А вы любите задачи на взвешивание?
1) Перед гномом лежат три кучки бриллиантов: 4, 5 и 6 штук. В одной из кучек лежит один фальшивый бриллиант. Все бриллианты имеют одинаковый вид, все настоящие бриллианты весят одинаково, а фальшивый отличается от них по весу. У гнома есть чашечные весы без гирь. Гному надо за одно взвешивание найти какую-нибудь одну кучку, в которой все бриллианты наверняка настоящие. Как это сделать?
2) Дан мешок сахарной пудры, чашечные весы и гирька в 1 г. Как за 5 взвешиваний отмерить 31 г сахарной пудры?
3) Известно, что в наборе из 32 одинаковых по виду монет есть две фальшивые монеты, которые отличаются от остальных по весу (настоящие монеты равны по весу друг другу, и фальшивые монеты также равны по весу друг другу). Как разделить все монеты на две равные по весу кучки, сделав не более 4 взвешиваний на чашечных весах без гирь?
Handbook of Neuroevolution Through Erlang: Справочник по нейроэволюции через Erlang
4.6 🌕🌕🌕🌕🌖 11
🥇Бестселлер: генетические алгоритмы, биоинформатика, научные исследования, Erlang
Handbook of Neuroevolution Through Erlang. Gene I. Sher. 2012
О книге
Книга «Handbook of Neuroevolution Through Erlang» объединяет теорию и практическую методологию создания систем вычислительного интеллекта на базе нейроэволюции с использованием языка Erlang. В вступлении Джо Армстронг, один из создателей самого языка, раскрывает ценность подхода и обосновывает выбор Erlang для таких задач. Читатель получает исчерпывающий пошаговый учебник по созданию современной платформы TWEANN (Topology and Weight Evolving Artificial Neural Network) - Топология и вес эволюционирующей искусственной нейронной сети.
Структура и методология
Материал выстроен от простейшего симулированного нейрона до полноценной системы, что позволяет освоить ключевые концепции без скачков в сложности. Каждый этап подробно описан и проиллюстрирован примерами кода на Erlang. Следуя руководству, можно самостоятельно собрать TWEANN для моделирования искусственной жизни или для автоматизированной торговли на рынке Форекс.
Практические сферы применения
Моделирование искусственной жизни и экосистем
Разработка алгоритмических торговых стратегий для Форекс
Управление автономными агентами и роботами
Почему Erlang
Парадигма конкурентного программирования через обмен сообщениями
Эффективное распределение задач на многоядерных и многопроцессорных системах
Архитектура, близкая к принципам эволюционных и нейрокомпьютерных моделей
Книга демонстрирует, как использовать встроенные возможности Erlang для задач машинного обучения и раскрывает реальные сценарии применения технологии в финансовых алгоритмах, симуляциях жизни и робототехнике.
Книга «Справочник по нейроэволюции через Erlang» (Handbook of Neuroevolution Through Erlang) доступна как на русском, так и на английском языках.
Алгоритм измерения уровня в цилиндрической ёмкости
Как-то стояла задача измерить уровень ёмкости воды. Ёмкость вертикальная — цилиндрическая. Этот уровень необходимо было перевести в объём воды. Хочу написать вам рабочий метод автоматизации уровня.
Приветствую всех посетителей сайта, с вами автор блога, Гридин Семен. Пишу статью про рабочую программу на отечественном оборудовании Овен ПР.
Емкость с водой
К сожалению фото с объекта не сохранились. В картинках покажу, какая примерно была емкость и что мы в неё врезали для измерения уровня.
Вот так вот она примерно выглядела. Определили высоту водяного столба. Снизу врезали датчик избыточного давления ПД100. В единицах 1 бар — это 10 метров водяного столба. Исходя из этих данных можно посчитать объем воды. Так как ёмкость у нас была округлой формы. В верхней и нижней части объемы отличались от среднего уровня.
Реализация алгоритма
Так как емкость была не совсем правильной формы, формулы по расчету объема здесь не сработали. Тогда мы сделали следующим образом — поделили диапазон тока 4-20 мА на определенное количество частей. Заливали мы бочку по расходомеру, и в каждой части записывали объем воды.
Зная высоту водяного столба и объём я склеил всё это в один мат. аппарат.
Использовал оборудование ОВЕН ИПП120 и ОВЕН ПР200. Почему именно так, всю информацию нужно было дублировать дистанционно.
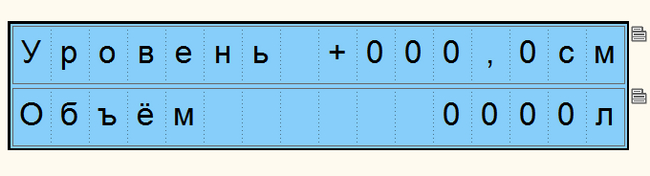
То что было на экране ИПП120 и ПР200.
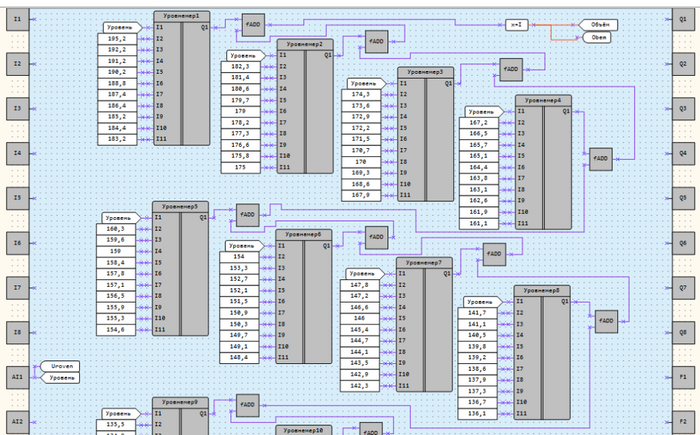
И вот таким вот образом склеивали показания уровня и требуемого объема.
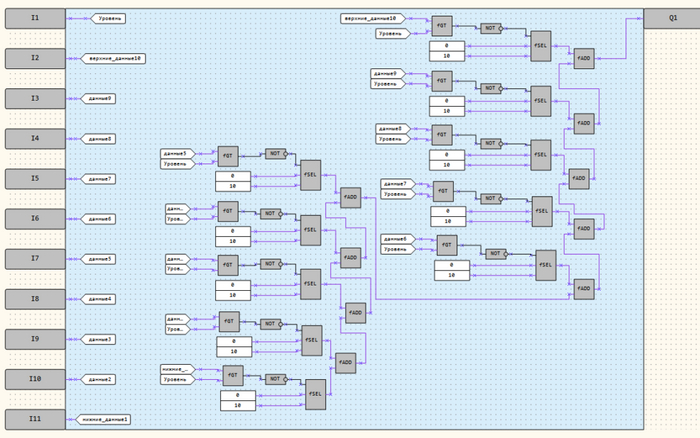
Внутренности блока Уровнемер.
У нас получилось достаточно точно. Так как делений много по всему диапазону датчика.
Если есть вариант, как сделать проще и лучше, напишите в комментариях. На этом я заканчиваю, пока-пока.
С уважением, Гридин Семен
Нужны ли программистам алгоритмы
Всем привет. Меня не раз спрашивали за мою карьеру, нужны ли программистам алгоритмы и структуры данных. Мнения об этом кардинально разные, кто-то считает, что дальше пузырьковой сортировки можно не идти, кто-то - что если вы за полчаса не набросаете алгоритм решения Судоку через бэктрэкинг, делать вам в программировании нечего. Мое личное отношение к этому вопросу постепенно менялось от начала карьеры ("нахер не надо, и так тонну всего учить") через середину ("бля, походу, все-таки надо, но впадлу") к нынешнему моменту ("алгоритмы это круто и интересно, учу по 4 часа в день, включая праздники и выходные"). Но нужны ли алгоритмы конкретно вам? Что ж, это зависит от постановки вопроса:
Нужны ли алгоритмы для того, чтобы стать программистом? Ответ простой - нет. Множество людей, включая меня, становились программистами, написав только ту самую пузырьковую сортировку. В целом на стадии становления программистом (если вы самоучка, университетская программа - другой вопрос с другими сроками обучения) они скорее даже вредны - сил будет потрачено ОЧЕНЬ много при сомнительном на этом этапе выхлопе. Хотя простенькие сортировки можно и глянуть.
Другой вопрос - нужны ли алгоритмы для того, чтобы стать хорошим программистом? Ответ - снова нет. Множество людей вполне успешно гоняют json'ы, шлепают CRUD'ы или формы без особых знаний об алгоритмах и структурах данных. При этом они могут писать вполне хороший, лаконичный, структурированный и покрытый тестами код. Хотя хорошему программисту все же лучше понимать, потому алгоритмы с time complexity >= O(N^2) - это плохо (не всегда и не везде), и как радикально может повлиять переход от O(N) к O(log N) на производительность.
Ок, двигаемся дальше. Нужны ли алгоритмы, чтобы получить хорошую работу? Ответ - не помешают, но не критичны. За все мое время работы в России меня где-то пару-тройку раз спрашивали по этой теме. В целом большинству компаний интереснее прогнать вас по более актуальным вопросам, чтобы убедиться, что вы знаете стек и можете как можно быстрее приступить к работе с как можно меньшим участием других прогеров. Исключение - Яндекс, там алгоритмы спрашивают железобетонно.
А вот нужны ли алгоритмы, чтобы получить очень хорошую работу? Ответ - однозначно да. Все, наверное, слышали про FAANG (MAANG). Вообще этим термином принято обозначать только входящие в него компании (Facebook/Meta, Apple, Amazon, Netflix, Google), но в целом есть еще пучок компаний типа Microsoft, Uber, Airbnb, Ebay и множество других, которые в акроним не поместились, но по зарплатам не особо уступают. Так вот - этим компаниям в массе своей глубоко пофиг на ваши знания разных фреймворков, очередей, баз данных и т.д и т.п - они достаточно велики и богаты, чтобы писать все себе самим (опять же, не везде и не всегда, но still). И алгоритмические задачи для них - по сути единственный способ проверить скилл кандидата. Правильный или нет - вопрос дискусионный, но прокачанный problem solving - это единственный способ получить такую работу.
Собственно, самым амбициозным можно начинать потихоньку сидеть на LeetCode / читать Кнута (Седжвика, Лафоре, etc) / проходить один из 100500 курсов на эту тему в интернете еще на этапе джуна. Остальным - по желанию и интересу.
Задача о ханойской Башне
Известная головоломка, которую придумал французский математик Эдуард Люка в 1883. Башня представляет из себя восемь дисков, нанизанных в порядке уменьшения размеров на один из трех колышков
Задача состоит в том, чтобы переместить всю башню на один из других колышков, перенося каждый раз только один диск и не помещая больший диск на меньший. Очевидно, что эта головоломка разрешима, но какой способ самый оптимальный? Какое количество является необходимым и достаточным?
Чтобы решить этот вопрос, нам следует чуть-чуть усложнить нашу задачу, а точнее обобщить ее, посмотрим, что будет в случае n дисков. Обозначим за T(n) - минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой. Очевидно, что T(1)=1, а T(2)=3.
Давайте найдем T(3), для этого надо перенести два верхних диска на средний колышек, затем перенести третий диск и на него перенести два других. Получаем 2*T(2)+1=7 перекладываний. Это легко обобщить на случай n дисков: сначала надо перенести n-1 меньших дисков на средний колышек, затем перенести большой диск и на него перенести n-1 меньших. Таким образом n дисков можно перенести за 2*T(n-1)+1 перекладываний. Но мы не доказали, что необходимо 2*T(n-1)+1 перекладываний
Действительно, нет ли более короткого пути? Оказывается нет. На некотором этапе мы переносим самый большой диск. Когда мы его переносим n-1 меньших дисков должны находиться на одном колышке, а для того чтобы собрать их вместе, потребуется по меньшей мере T(n-1) перекладываний. После перемещения самого большого диска в последний раз (его могут перемещать и больше одного раза) мы обязаны переместить n-1 меньших дисков обратно. Это требует T(n-1) перекладываний. Следовательно T(n) не меньше, чем 2*T(n-1)+1
Хорошо, мы получили равенство T(n)=2T(n-1)+1, кроме того мы знаем, что T(1)=1, совокупность таких равенств называется рекуррентностью. В данном случае легко угадать решение методом пристального взгляда: T(1)=1, T(2)=3, T(3)=7, T(4)=15, T(5)=31, T(6)=63. T(n)=2^n - 1? Это равенство легко проверить с помощью метода математической индукции.