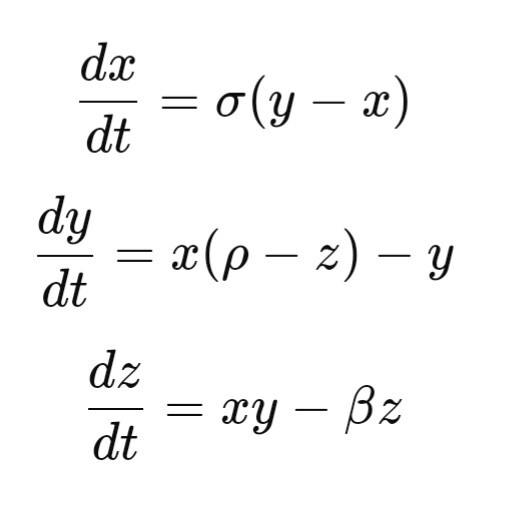Теория Хаоса: Наука о Непредсказуемом Порядке
Опираясь на прошлый пост, в котором мы описывали эффект бабочки как пример чувствительности к начальным условиям, давайте разберём, как он укладывается в общую концепцию теории хаоса. Поехали.
Что такое Теория Хаоса?
Теория хаоса — это исследование сложных систем, которые, хотя кажутся случайными, обладают внутренним порядком. Она описывает, как небольшие изменения в начальных условиях (тот самый эффект бабочки) могут привести к огромным различиям в результате, делая поведение системы почти непредсказуемым. Примеры таких систем: погода, рост популяций, финансовые рынки и даже движение планет.
Как теория хаоса родилась из эффекта бабочки?
Основоположником теории хаоса стал метеоролог Эдвард Лоренц, который в 1961 году заметил, что округление чисел в его компьютерной модели привело к совершенно иным прогнозам погоды. Он описал это как «эффект бабочки» — маленькие различия, подобные взмаху крыла бабочки, могут вызвать мощные изменения, вроде урагана, который мог бы развиться или не развиться в зависимости от этих незначительных изменений.
Пример в математике: уравнения Лоренца
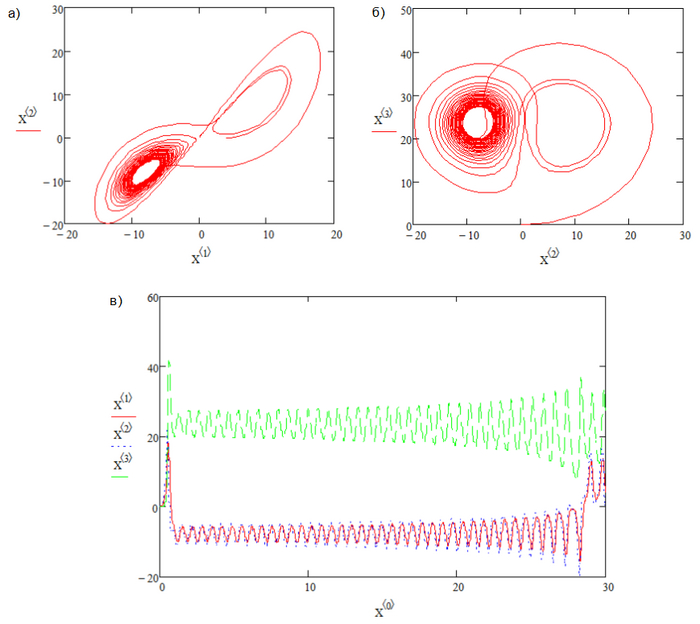
Уравнения Лоренца, которые он использовал для моделирования атмосферы, оказались примерами «динамической системы», чувствительной к любым, даже минимальным изменениям. Формулы:
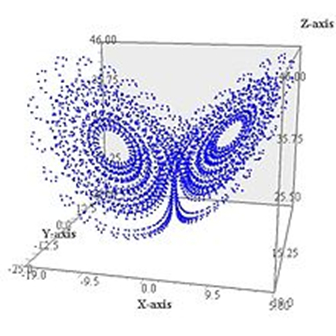
где 𝜎, 𝜌 и 𝛽 — параметры, которые делают систему хаотичной при определенных значениях. График траекторий этих уравнений напоминает форму крыльев бабочки — отсюда и визуальный символ теории хаоса.
Применение Теории Хаоса
Сегодня теория хаоса применяется в самых разных сферах: от экономики и биологии до метеорологии и астрофизики. Она помогает моделировать сложные процессы, где даже малые изменения могут вызвать значительные последствия. К примеру, при изучении изменений климата или экосистем теорию хаоса используют для прогнозирования сложных взаимосвязей.
Заключение
Теория хаоса показывает, что даже в кажущемся хаотичном мире существует скрытая система. Малейшие изменения могут создавать мощные последствия, что заставляет нас иначе смотреть на окружающий мир и ценить кажущуюся незначительность начальных условий.
Литература и Научные Работы
— Эдвард Лоренц. Deterministic Nonperiodic Flow, Journal of the Atmospheric Sciences (1963). Это фундаментальная работа Лоренца, с которой началась теория хаоса. Лоренц описал в ней ключевые принципы, включая влияние малых изменений начальных условий.
— Стивен Строгатц. Nonlinear Dynamics and Chaos (1994). Книга, доступно объясняющая основные принципы нелинейной динамики и хаоса для начинающих. Она помогает понять сложные идеи через примеры и иллюстрации.
— Митчелл Фейгенбаум. Quantitative Universality for a Class of Nonlinear Transformations, Journal of Statistical Physics (1978). Фейгенбаум сделал революцию в теории хаоса, описав универсальные константы, которые повторяются в различных хаотических системах.
— Джеймс Глейк. Chaos: Making a New Science (1987). Эта книга популяризировала теорию хаоса для широкой аудитории. Глейк рассказывает историю развития этой науки и ее влияние на разные области знаний.
Продолжение рассуждений о "сложности" и математике
Я понимаю что с точки зрения теории эволюции , чтобы существо изменилось нужно чтобы изменилась среда в которой он живет.Например если вдруг зимы исчезнут с нашей планеты , то зайцу беляку больше не нужна будет белая окраска зимой, потому что снега зимой вокруг больше нет и выгоднее быть серым. Соответственно для того чтобы существо усложнилось , необходимо чтобы среда вокруг него тоже поменялась. На примере человека и его мозга , это означает - раз мозг постоянно увеличивался и усложнялся ,то среда вокруг него постоянно менялась . Более того я могу предположить что сам человек отчасти менял эту среду , например обзавелся костром , пещерой , языком и еще тысячей интересных предметов вокруг себя. При этом я знаю что есть существа среда жизни которых совершенно мало меняется и они также мало изменились за последние пару миллионов лет. Например крокодилы. Интересно что и в математике есть поведение похожее на то что я описал выше. Например алгоритмы . Предположим программист пишет программу для компьютера результат вычислений которой , он будет использовать для следующего вычисления. Например программа берет на вход цифру 2 и умножает ее на 2 , результат получается 4 , затем он берет 4 и опять умножает на 2 и так далее...То есть в каждый новый момент времени у него результат меняется. Если считать его алгоритм живым организмом , а результат после каждого вычисления состоянием среды в каждый момент времени , то можно сказать что его живое существо меняет среду вокруг себя , причем делает это предсказуемо. Если же задаться вопросом , для всех ли программ программист сможет предсказать как будет меняться среда не выполняя код алгоритма , то ответ на него уже есть в математике , и ответ этот - нет (проблема точки останова). Также с точки зрения логики , на самом деле я могу создать три типа алгоритмов взаимодействующих со средой - те которые среду не меняют , те которые меняют среду периодично ( например вычисление в виде десятичной дроби рационального числа) , и те которые меняют среду не периодично (например вычисление иррациональных чисел - числа пи(хоть его и можно вычислять с любой позиции , тем не менее Формула Бэйли — Боруэйна — Плаффа O(n logn) в смысле сложности)) . Появляется вопрос , а какому алгоритму или его типу соответствует задача увеличения мозга человека? Если начинать задумываться об этом вопросе то во первых этот алгоритм желательно должен менять среду не предсказуемым образом. Это означает что человек не имеет возможности узнать как он будет смотреть на мир через сто лет , потому что если бы он мог это сделать сейчас то он бы так начал думать сейчас. Соответственно этот алгоритм либо принадлежит классу алгоритмов вычисляющие в качестве среды сверхдлинные периодические числа (потому что мозг развивается миллионы лет) , либо классу алгоритмов вычисляющих иррациональные числа.
Также я понимаю , что естественная среда обитания человека очень связана с динамическими системами как разделом математики. Если человек живет в лесу к примеру , то его выживание зависит от всех предметов вокруг него и как они взаимодействуют друг с другом во времени. Например человек наблюдая за дикими пчелами и развитием их поведения во времени может их одомашнить. И тут тоже есть интересное совпадение предыдущих рассуждений с математикой. Динамические системы делятся на стационарные , системы с циклами , и без циклов. И в принципе это логично потому что алгоритмами можно реализовать много функций порождающих динамические системы. Однако в теории динамических систем есть крайне интересное состояние называемое хаосом. На примере человека живущего в лесу (если бы в лесу было состояние хаоса) означало бы , что любое действие которое он сделал бы в этом лесу имело отдаленные и серьезные последствие для леса в будущем (эффект бабочки). Что возможно бы означало что мозгу человека необходимость постоянно учитывать самые мелкие детали в окружающем пространстве для предсказания будущего ( а значит расширять свою память) связана с теорией хаоса. Такой вот вывод.
В целом я не до конца уверен в выводах связанных с теорией хаоса , хотя бы потому что хоть и внимание человека хоть и сильно но мы постоянно не замечаем многие детали вокруг нас ну и хаос особое состояние, однако мне нравится что у меня появилась гипотеза почему самая мелкая деталь может повлиять на всю нашу жизнь , а значит мозгу все равно приходится учитывать мелкие детали.
Теория Хаоса
Официальное определение
Тео́рия ха́оса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных, при определённых условиях, явлению, известному как хаос (динамический хаос, детерминированный хаос). Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной. Для акцентирования особого характера изучаемого в рамках этой теории явления обычно принято использовать название теория динамического хаоса.
В среднем теория детерминированого хаоса выглядит так.
Расширение кругозора и другое объяснение и понимание истинного Хаоса.С "налетом" квантовой запутанности сознания.
Определение под спойлером.
Хаос - в хаосе нет правил — есть только выборка(граница).Ее можно назвать форма, а все остальное неформа. Полное описание форма(не).Так как форма нужна чтобы понять (не) и понять что () это границы, слово форма слева как изначальное.
Остальное в сериях статей Движок Материи(Глоссарий)
Начальные постулаты.Выглядят абстрактными, имеют смысл - фильтр готовности сознания к самонаблюдению, выходу за область определения сознания(шаблона восприятия).Если неприятно - читать не надо.
Все существует. Ничего делать не надо.
Зависимый наблюдатель
Неслучайность
Нет правил — тоже правило.
Ниже представлены две теории
Выборка хаоса с вектором (правилом)
1.Поглощающая временная теория вибрационного хаоса
Выборка истинного хаоса с объяснением(пониманием) относительно появления границ (точки) и мысли об этом
2.Самоопределяемая безвременная теория вибрационного хаоса
Начало описания теории
Вводная
В хаосе нет правил — есть только выборка(граница).Ее можно назвать форма, а все остальное неформа. Полное описание форма(не).Так как форма нужна чтобы понять (не) и понять что () это границы, форма слева как изначальное.
В хаосе нет никаких векторов и законов распространения. Принцип определяется выборкой. Хаос с принципами — творение в(и)з истинном хаосе. Выборку форма(не) можно назвать представлением системы координат истинного Хаоса Ничто Пустоты Абстракции Непредставимого Трансдентного Осознаного Математической Точки Ноль Области Неопределения.
1/05/2011
Поглощающая временная теория вибрационного хаоса
Определения
Волновой процесс - совокупность проявленного и непроявленного порожденная изначальным ХАОСОМ. Того НИЧТО - что есть ВСЕ. Имеет волновые характеристики. Приближенно соответствует понятию "белый шум" электротехники.
Существо - волновой процесс имеющий общность(единство)
Вибрация = проявленное и непроявленное в точке.
Зарождение
Однажды в океане распада и рождения появилось что то, что могло вибрировать - распадаться и рождаться в унисон.
Процесс толкал другие "точки". "Точки" начинали вибрировать как процесс, становясь процессом. Он "питался" ими. То что родилось было первым существом. Первым "вампиром".
Эволюция
Существо было не одно. Таких существ было множество. Каждое вибрировало в унисон. Но вибрации были различны. Каждое существо поглощало все что было рядом. И чем больше они становились, тем мощнее были их вибрации. Эта общность стала волновым процессом.
Волновые процессы родившиеся в результате этого называются сейчас - сознанием. Сознания поглощали другие сознания. Это были вампиры. Все что существует есть поглощение(вампиризм) в чистом виде.
Вселенная
Сознания порожденные ХАОСОМ имели разные вибрации. В зависимости от того, как они вибрировали возникали различные слои. Материальная вселенная одна из них.
Вампиризм
Целью любого сознания является поглощение других сознаний для того чтобы стать единым сознанием. Такое развитие идет как сверху вниз так и снизу вверх. Это и есть "вампиризм".
Для того чтобы поглотить что либо сознания дают возможность другому сознанию разделить общность - вибрировать одной вибрацией. Получить резонанс. Это и есть вампиризм
Сознание то кем себя считает. И то к чему себя относит. "Вампиризм" - есть основа существования всего. Феерия пожирания и расширения АБСОЛЮТА
Способа избежать общности два:
1.Полное НИЧТО и РАСПАД. Но он невозможен так как зарождение снова повторится как и было ранее.
2.Создание своей общности "творение"- поглощение других сознаний путем создания с ними общностей.Единение.Целосность.Победит в этом тот кто имеет вибрации выше-общность больше.Выиграет только творец.Творите -это ВАША ЦЕЛЬ
Люди
Люди,(как впрочем и все остальные) - корм существующих сознаний на всех слоях. А также часть общности сознания людей.
Возможно, люди и смогут стать единым, тем самым вампиром ,что поглотит остальные общности.
24.05.2023
Самоопределяемая безвременная теория вибрационного хаоса
Точка — точка без формы(измерений, координат).Вне(без)пустота(ничто)( ). Абстракция. Непредставимо.Неощутимо. Самоопределяема как уникальный идентификатор выборки хаоса. Истинного хаоса.
Волновой процесс - совокупность проявленного и непроявленного порожденная изначальным ХАОСОМ. Того НИЧТО - что есть ВСЕ. Имеет волновые характеристики. Приближенно соответствует понятию "белый шум" электротехники.
Существо - волновой процесс имеющий общность(единство)
Вибрация = проявленное и непроявленное в точке.
Зарождение
Однажды в океане распада и рождения появилось что то, что могло вибрировать - распадаться и рождаться в унисон.
Процесс объединял "точки". "Точки" вибрировали как процесс. То что родилось было существом
Эволюция
Существо было не одно. Таких существ было множество. Каждое вибрировало в унисон. Но вибрации были различны. И чем больше они становились, тем мощнее были их вибрации. Так общность стала волновым процессом.
Слияние происходило при одинаковой мощности вибрации существа это и есть резонанс, а мощность вибрации общности стала называется спектром волнового процесса.
Волновые процессы родившиеся в результате этого называются сейчас - сознанием. Сознания объединяли другие сознания. Все что существует есть объединение в чистом виде.
Вселенная
Сознания порожденные ХАОСОМ имели разные вибрации. Вибрации соединялись в унисон порождая волновые процессы. В зависимости от того, как они вибрировали возникали различные слои имеющие свой спектр. Материальная вселенная одна из них.
Творение
Все что НИЧТО что есть ВСЕ уже существует. Творение это акт слияния с волновым процессом уже существующем в хаосе.
При взаимодействии двух существ происходит резонанс, но уникальная вибрация сущности остается неизменной. Спектр растет. Мощность вибрации удваивается
Любая мысль идея форма чувство все что оказалось в изначальном сознании сущности при резонансе с другой сущностью (творением) является памятью нового волнового процесса что вызывает повышение спектра соотвественно.
Память тем больше чем больше резонансов. Происходит постоянное пополнение памяти и увеличение спектра волнового процесса.
Важно понимать что определение спектра и вибрации сознания лишь малая часть осознания мира. Все предметы, явления, законы, информация и формы есть волновые процессы.
Практика
Что такое теория хаоса? Рассказывает журнал «Лучик»
При словах «теория хаоса» многие вспоминают математика из фильма «Парк Юрского периода». Тот пытался объяснить смысл теории хаоса с помощью капли воды, скатывающейся по большому или указательному пальцу.
Последовавшие затем в фильме события заставили многих думать, что теория хаоса – это что-то вроде Закона Мерфи: если неприятность может случиться, то она случается. Это неправильно. Математик в фильме говорил о другом. Почему случается неприятность? Потому что всё предусмотреть невозможно.
Вот это в целом правильно и совершенно понятно. Непонятно только, для чего же тут понадобилась целая теория? Вот это мы и попробуем объяснить.
Неудача Пифагора
В Древней Греции хаосом называлось первоначальное состояние вселенной – когда не существовало ни света, ни тьмы, ни жизни, ни правил и законов. А сотворение мира с точки зрения древних греков представляло собой переход от хаоса (беспорядка) к космосу (порядку).
Одним из образцов идеального порядка, полного «космоса», для древних греков была математика. Пифагор создал целую философскую систему, в которой главное место занимали «божественные числа». «В математике, – говорил Пифагор, – нет места хаосу, то есть случайности и беззаконию. А значит, люди должны жить по законам математики».
Учение Пифагора стало настолько популярным, что он и его ученики даже захватили власть в городе Кротоне. Но... простым горожанам совсем не понравилось, когда их «оцифровали». Произошло народное восстание – и пифагорейцев изгнали из города.
Но понятие математически правильного, предсказуемого порядка прижилось. Периодически людям начинает казаться, что можно создать социальную систему, в которой все «неопределённые» и «расплывчатые» морально-нравственные и культурные нормы будут заменены строгими законами и алгоритмами. Очередной всплеск таких представлений мы переживаем сегодня.
Если есть законы, которым подчиняются все явления природы, то должны быть законы, которым беспрекословно должны подчиняться все люди. Так же мы с вами рассуждаем, правда?
Теория Лапласа
Во времена позднего Средневековья начался расцвет механики. Мастера того времени научились создавать удивительные (даже по нашим меркам) механические диковины.
Это были и часы, которые могли предсказывать астрономические явления, например, фазы Луны или затмения Солнца. Это были и разнообразные механические куклы – например, известно описание фигурки мальчика, который прекрасным почерком писал текст на бумаге.
Механика с её сложной системой приводных колёс, рычагов, шестерёнок, пружин и маятников показалась людям настоящим образцом того самого «порядка», которому подчиняется Вселенная.
Своё математическое описание механика получила в основном благодаря работам французского учёного Лапласа. Именно он начал любое явление рассматривать в качестве динамической системы, то есть системы, свойства (параметры) которой изменяются во времени. Для каждого элемента такой системы (например, отдельной шестерёнки в механизме часов) можно указать некое правило, формулу, которая называется законом движения.
Достигнутые результаты привели Лапласа в такой восторг, что он заявил следующее (читаем внимательно):
«Если для некоей динамической системы известны состояние в момент времени t и закон движения, мы сможем безукоризненно точно сказать, в каком состоянии эта система была в прошлом и в каком состоянии она будет находиться в будущем».
Учёный даже описал мифическое существо, которое знает всё прошлое и всё будущее всего существующего во Вселенной – позднее это существо стали называть «демоном Лапласа».
Итак, согласно Лапласу, любая динамическая система ведёт себя, как механические часы. Будь жив Пифагор, он, наверное, очень бы порадовался – ведь теоретическая механика Лапласа была идеальным воплощением пифагоровского математически правильного «космоса». Всё на своих местах, всё раз и навсегда предопределено, всё по строгому расписанию, никаких неожиданностей, никакого хаоса!
Что-то не то...
Надо сказать, что и во времена Лапласа многие учёные к «механической» концепции отнеслись отрицательно. «Ну хорошо, – говорили они, – с механическими машинами это справедливо. А можно ли с помощью вашей теории предсказывать погоду? А как насчёт человеческих отношений – дружбы, вражды?»
Теория Лапласа испытывала проблемы не только с прогнозом погоды или человеческими отношениями. Дело в том, что в математике того времени тоже были сделаны важные открытия, которые концепциям Лапласа ну никак не хотели подчиняться!
Случайные процессы
Первым таким открытием стало создание теории вероятностей – области математики, изучающей случайные процессы. Например, бросание игральных кубиков. Сколько на следующем броске выпадет очков? Можно ли это предсказать с помощью математики? Нет, нельзя.
Хуже того – в дальнейшем оказалось, что математически невозможно вообще описать такое понятие, как случайное число. Любой из нас с лёгкостью придумает какое-нибудь случайное число – а вот написать математическую формулу, которая это случайное число описывает, оказалось невозможно в принципе!
Вторым открытием стал закон всемирного тяготения Ньютона. Довольно простая формула, её в школе в седьмом классе проходят. Но дело в том, что эта формула описывает поведение динамической системы, состоящей из двух тел – например, Земли и Луны. Или Земли и Солнца. Но на самом-то деле таких тел намного больше! Земля притягивает Луну, а Солнце притягивает Землю – но ведь Луну Солнце тоже притягивает, правда? А когда математики попробовали с помощью формулы Ньютона решить задачу для трёх тел, они столкнулись с невероятными сложностями!
Точное общее решение этой задачи не найдено до сих пор.
Теория хаоса
Внимательно изучая эти и другие задачи, к концу XIX века учёные пришли к выводу, что большинство динамических систем в нашей вселенной ведут себя совсем не так, как это описывал Лаплас. Даже если эти системы описываются с помощью простых и точных формул, в итоге их поведение оказывается непредсказуемым – хаотическим!
Так на свет появилась математическая теория хаоса. Или, если говорить правильнее, детерминированного хаоса.
Возьмём, например, движение Луны вокруг Земли. С одной стороны, оно описывается простой формулой – законом всемирного тяготения Ньютона. Луна вращается вокруг Земли по орбите. Но при этом рассчитать точное положение Луны на орбите не получается, хоть ты тресни!
Современные астрономы используют для расчётов особые, очень сложные формулы (в математике такие формулы называют рядами), причём числовые параметры этих формул постоянно уточняются и исправляются на основании реальных наблюдений в телескоп.
Другой пример – погода. С одной стороны, погода на нашей планете – это всего лишь перемещения масс воздуха. И параметров тут всего три – это температура, скорость и влажность. И описываются эти параметры довольно простыми математическими формулами. Только простота формул в итоге ничего не даёт, – как известно, даже прогноз погоды на завтра может ошибаться. А уж предсказать более-менее точно погоду в следующем месяце вам не возьмётся ни один метеоролог. Так что никакого расписания, никакой предопределённости, сплошные сюрпризы и самый натуральный хаос!
Линейность и нелинейность
Почему такая динамическая система, как часы, ведёт себя «по Лапласу», то есть идеально правильно, а погода – нет?
Как показали исследования, хаотической может быть только нелинейная система.
Две сцеплённые между собой одинаковые шестерёнки – это классический пример линейной системы: если мы начнём быстрее вращать одну шестерёнку, автоматически начнёт вращаться быстрее и другая. Причём во сколько раз быстрее мы будем вращать первую, в точности во столько же раз ускорится вторая. Такая система линейна, а потому хаосом быть не может.
А вот в случае с погодой параметры независимы друг от друга: если, скажем, мы увеличим скорость ветра в два раза, ведь его температура при этом не станет в два раза выше, правда?
Возьмём ещё один пример. Допустим, рабочий делает на станке детали и получает деньги за каждую изготовленную деталь. Если он начнёт работать в два раза быстрее, то сделает в два раза больше деталей и получит в два раза больше денег. Такая система линейна, в ней зарплата линейно зависит от скорости работы.
Но заменим теперь рабочего на, скажем, телеведущего. Допустим, телеведущий решил говорить во время выпусков новостей в два раза быстрее – как вы считаете, прибавят ему за это зарплату в два раза? Данная система нелинейна.
Эфффект бабочки
Другой важный вывод, к которому пришла теория хаоса, следующий. При малом расхождении начальных условий динамической системы разброс её конечных состояний может быть очень большим. Что это означает?
Если взять механические часы и повернуть чуть-чуть одну шестерёнку, то вторая, сцеплённая с ней, тоже повернётся чуть-чуть. А вот в хаотических системах совсем не так!
Например, лежит снег на склоне горы. Одна снежинка чуть-чуть подвинула две другие, эти две немножко подвинули соседние – и через 5 минут по склону несётся с огромной скоростью чудовищная лавина снега!
Это явление часто называют эффектом бабочки. Объясняя студентам теорию хаоса, американский учёный Лоренц приводил пример, когда «взмах крыла бабочки где-то над Америкой может в результате сложной цепи событий привести к урагану над Тихим океаном».
Время Ляпунова
Третий важный вывод теории хаоса – ограниченность возможности предсказания состояния системы в будущем. Для каждой хаотической системы существует некое время, называемое временем Ляпунова, за пределами которого её поведение становится полностью непредсказуемым.
Что это означает? С помощью формул и расчётов мы можем в какой-то степени предсказать поведение динамической системы – но только до определённого момента! Скажем, местный гидрометцентр может дать надёжный прогноз погоды на ближайшие 2 часа. Вполне приличный прогноз – на ближайшие 6 часов. Более-менее приемлемый – на завтра. Однако уже прогноз погоды на 3–4 дня вперёд достоверным не будет!
Другой пример – наша Солнечная система. С одной стороны, она управляется по законам небесной механики, и учёные могут очень точно предсказать движение планет, спутников и других небесных тел. Да, это так – но со временем эта точность падает! Для Солнечной системы время Ляпунова составляет 50 миллионов лет – а это значит, что предсказать положение планет и их спутников на 50 миллионов лет вперёд (пускай даже хоть сколько-нибудь приблизительно!) мы не в состоянии. Вообще! Никак!
Так что никакого всезнающего «демона Лапласа» (или «искусственного интеллекта», как сейчас это принято называть) быть не может. Причём не может быть именно согласно науке, на которую так любят ссылаться сторонники «тотальной цифровой трансформации».
Это была статья из журнала «Лучик». Познакомиться с журналом можно по ссылке. В мартовском номере журнала читайте:
Зачем человеку подвиг? О Сократе, Сикстинской Мадонне и Александре Матросове
Русские дети. Читаем стихотворение Некрасова и думаем
Почему над мудрецами, ощупывающими слона, смеются глупцы?
Подписаться на мартовский номер «Лучика» можно до 20 февраля по ссылке
Как ожидать неожиданное (4)
Заканчиваем знакомиться с книгой Кита Йейтса.
Экспонента – это когда ответ усиливает стимул. Но бывает и наоборот. То есть обратная связь может быть отрицательной. В пиаре этот феномен получил название эффекта Барбары Стрейзанд. Судебный иск артистки с целью изъять фото своего роскошного дома из публичного доступа привело к обратному эффекту: практически никого не интересовавший дом Стрейзанд начали смотреть все, кому не лень. Число просмотров выросло с шести до полумиллиона.
Более широко в психологии это называется эффектом бумеранга: так берут на «слабо» и идут против запретов. Нежелательный ответ может вызвать неправильно выбранный стимул. Стремление избавиться от кобр в Дели привело в своё время британскую колониальную администрацию к решению платить за каждую сданную убитую кобру. Выход нашёлся быстро: индусы стали разводить кобр на убой. Англичане отменили награду, и куда выпустили эти все террариумы? Правильно, в окрестности Дели. Прошли века, и бывшие колонизаторы встали на те же грабли: уже в наши дни они стали платить за уничтоженные плантации опийного мака в Афганистане. Афганцы кассировали и со снятого урожая, и с уничтожения поля после этого. Ну а потом высаживали плантации на новом месте. Оплата американскими властями каждого построенного километра железных дорог привела к тому, что компании, ведущие строительство навстречу друг другу, намеренно «промахивались», идя параллельным курсом. Примерам подобных манипуляций несть числа: здесь колумбийские военные отчитываются за борьбу с партизанами трупами убитых гражданских, там учителя подделывают оценки своих учеников, а ещё где-то больница не хочет лечить сложных пациентов, не желая испортить себе статистику. Закон Гудхарта в действии:
Когда мера становится целью, она перестает быть хорошей мерой
К нежелательным последствиям может привести тренировка нейронных сетей. Подобные системы, натренированные на определённых наборах данных, представляют собой чёрные ящики: мы не знаем внутреннюю логику, на которой строятся решения системы. Это, конечно, риск: кто знает, как поведёт себя система в новых обстоятельствах? У неё есть заданная нами цель, а вот выбор средств часто явно не указывается. Автор рассказывает историю, как нейронку по рентгенодиагностике тренировали на данных из двух больниц, статистика в одной из которых заметно превышала другую. Система научилась различать происхождение снимков и базировать свои выводы на этом. Ведь ей скармливали весь снимок, включая вспомогательную информацию на полях. А то, что надо смотреть лишь на лёгкие, а не буквы L и R, не сказали.
При выработке модели важно также не зайти слишком далеко. Можно интерполировать последовательность 3, 5, 7, 9 простой линейной функцией и заключить, что следующее значение – 11. Но эта функция – не единственная с такими значениями. Через эти точки можно, например, провести кривую четвёртого порядка, следующее значение которой будет 23. Что делать? Не плодить сущности понапрасну и пользоваться бритвой Оккама. То есть использовать минимальное число параметров для объяснения ситуации. В том числе не стремиться подогнать модель под данные с идеальной точностью.
Упомянув про самосбывающееся, трудно пройти мимо пророчества самоотменяющегося. С подобной дилеммой столкнулся ещё пророк Иона в седой древности: Господь повелел ему передать пророчество о разрушении Ниневии, если жители этого города не раскаются. Однако вот ведь какое дело: если они поверят ему и раскаются, то город не разрушится, и тогда само пророчество не сбудется. Ну и кто он будет после этого в их глазах? Вот и попытался спетлять и отправился в плаванье. Но Господа не обманешь. Корабль попал в сильнейший шторм, и когда корабельщики бросили жребий, кого выкинуть за борт, тот пал... да, на Иону. Как только того выбросили, шторм прекратился. Но Иона не погиб в пучине: его проглотил кит, в чреве которого три дня и три ночи он молился. Господь дал ему второй шанс, кит изверг Иону на берег, тот пошёл в Ниневию, стал пророчить о гибели города через сорок дней. Ниневийцы впечатлились и покаялись, их гибель не случилась, а пророчество Ионы – не исполнилось. Автор находит Иону в современности в лице эпидемиолога Нила Фергюсона, предсказавшего смерть полумиллиона британцев, если не бороться с распространением коронавируса. До такого не дошло. Умерло порядка двухсот тысяч. Помог локдаун, вакцинация и другие меры, за которые и выступал Фергюсон. Автор, правда, не сообщает ещё одну цифру из его предсказаний: что при соблюдении карантина число жертв может упасть ниже 20 тысяч.
К неожиданному исходу соперничества может привести недооценка противника. Голиаф может почивать на лаврах и расслабиться, в то время, как Давид будет гореть желанием опровергнуть ожидания и самоутвердиться своей победой над фаворитом. Подобный феномен автор называет эффектом аутсайдера, хотя Википедия имеет в виду нечто другое. Так или иначе, такое развитие событий, наряду с самоотменяющимся пророчеством, представляет собой примеры отрицательной обратной связи.
Если честно, я так не считаю. Это, скорее, примеры того, когда исход не такой, как планируется. Сигнал же обратной связи вычитается из задания на управление для вычисления рассогласования, чтобы узнать, далеко ли мы от цели. Мы выстреливаем в мишень, смотрим, куда попала пуля и делаем поправку. Стоим под душем, крутим ручку и чувствуем изменение температуры. Температуру (а также другие параметры тела) регулирует и наш мозг, используя обратную связь и управляющие воздействия. Разумеется, исход процесса регулирования может оказаться не таким, как хотелось бы. Длинная труба в душе может сделать задачу сложной, мы крутим кран в одну сторону, но пока вода достигнет нашего тела, проходит слишком много времени, и станет слишком горячо. Крутим в другую – опять промахиваемся, слишком холодно. Система входит в колебания. И будет неплохо, если эти колебания не слишком широки. А то при определённых обстоятельствах система может пойти вразнос.
Совет автора читателю очевиден до невозможности: пытаться предвидеть эффект бумеранга. Думать о непредвиденных последствиях. Брать на «слабо». Не всегда идти путём прямых запретов, ведь запретный плод сладок. Практическая ценность таких советов, на мой взгляд, не слишком высока.
Каковы бы ни были наши потенциальные предсказательные способности, иногда приходится признать: они не бесконечны. Приведу пример. Допустим, что совершая действие A, мы уменьшаем какой-то параметр B, который неизбежно должен уменьшить параметр С, что нам и нужно. Но на самом деле наше действие может привести и к росту параметра D, который тоже влияет на C. Единственным способом убедиться в нужном результирующем воздействии этих двух путей влияния будет использование количественной модели. Вербальная качественная модель в этом случае не сработает.
Говоря о непредсказуемости, автор упоминает заблуждение нормальности: мы склонны думать, что в будущем всё будет так же, как сейчас. Мы откладываем написание завещаний, не сразу реагируем на предупреждения о надвигающемся бедствии. Некоторые даже не верят предупреждениям. Чем это чревато, мы можем убедиться на примере судьбы жителей Помпейи, которые даже после начала извержения Везувия далеко не все поспешили покинуть город. Наши современники не намного разумнее их, что показала реакция жителей Нью-Йорка и окрестностей на штормовое предупреждение в октябре 2012 года. Тогда лишь менее половины жителей покинуло зону эвакуации. Результат: смерть 159 человек в результате урагана Сэнди.
Кстати, о погоде. Её мы хоть и умеем предсказывать, но тоже неидеально. Когда-то давно мы полагались на эмпирические приметы вроде красного неба на закате, предвещавшего ясную погоду (в отличие от красного восхода). Эта примета нашла своё отражение даже в Библии.
На закате, увидев, что небо красное, вы говорите: «Будет хорошая погода», а на рассвете, если небо заволокло багровыми тучами, вы говорите: «Будет буря».
Нельзя не отказать Иисусу в правоте: действительно, в умеренных широтах Северного полушария преобладают западные ветры, и область высокого давления с хорошей погодой (которую мы видим как красное небо) появившись на закате, с большой вероятностью пройдёт через нас. Если же мы увидим красное небо на востоке, то, похоже, хорошая погода от нас уже уходит. Красный цвет небу придаёт преломление солнечных лучей в частичках пыли, застревающих в атмосфере при антициклоне.
Но не все приметы выдержали испытание временем. Коровы ложатся на землю по разным причинам, и совсем необязательно перед дождём. Натуралисты в Германии подметили в восемнадцатом веке, что древесные лягушки залезают вверх по деревьям в хорошую погоду. Появилась мода заводить у себя дома лягушку и держать её в кувшине, из которого наверх вела вверх маленькая лестница.
На самом деле, эти животные не предсказывали, а следовали хорошей погоде, при которой мошкара поднимается выше от земли. Разумеется, в домашних условиях своим поведением они не сообщали хозяину ничего путного. А синоптиков на телеэкране немцы иронически по сей день называют «погодными лягушками».
Поводов для иронии и издевательств над синоптиками сегодня тоже хватает, хотя стоит заметить, что мы лучше помним их неудачи, нежели их успехи. Ещё одним поводом для насмешек может являться неясность некоторых понятий. Вы знаете, что такое вероятность осадков? Это не просто вероятность дождя в определённом районе. Её нужно ещё умножить на процент площади с дождём в данном регионе. То есть если в Москве завтра точно будет дождь, но лишь на 75% площади, то вероятность дождя и будет 75%. Стоит знать, что некоторые коммерческие бюро погоды сознательно округляют вероятности осадков в большую сторону: лучше перебдеть и не дать клиенту промокнуть. Далее, они неохотно снимают дождевой прогноз в случае изменения обстоятельств в лучшую сторону: частые изменения прогноза подрывают доверие публики. Вообще, синоптикам и прочим прогнозистам имеет смысл представлять грядущее развитие событий в виде диапазона возможных сценариев с соответствующими вероятностями вместо какого-то одного наиболее вероятного сценария. Чем меньше будет недосказанностей – тем лучше.
Существование закона причины и следствия побудила Лапласа предположить создание супер-интеллекта – демона Лапласа – который бы на основе имеющейся в его распоряжении информации о Вселенной смог бы предсказывать будущее. Если это возможно, то свобода воли – всего лишь фикция. На самом деле, мало того, что у нас не хватит вычислительных мощностей, но и присутствуют фундаментальные вещи, ограничивающие наше точное знание координат и импульса частицы в данный момент времени. А именно принцип неопределённости Гейзенберга.
Так что синоптики, несмотря на определённый прогресс, никогда не смогут порадовать нас прогнозом стопроцентной вероятности. Не только по вышеизложенной причине, но и в силу чувствительности их моделей к изменению начальных условий. Погода – это не как у Жванецкого, у которого из консерватории неизбежно попадаешь в Сибирь. Наоборот. Здесь мы имеем дело со сложной системой. Мы можем очень точно рассчитать состояние подобной системы в будущем. Но стоит измениться начальным условиям совсем чуть-чуть – и прогноз окажется совсем другим.
В шестидесятых годах прошлого века американский математик и метеоролог Эдвард Лоренц создал простую модель атмосферы, которую обсчитывал на своём компьютере. Распечатки результатов выдавались с точностью до третьего знака после запятой, в то время, как внутреннее представление чисел в компьютере имело шесть знаков. Однажды Лоренц захотел повторить свои вычисления, но поленился делать всё с самого начала, а использовал распечатки промежуточных результатов. Он с удивлением обнаружил, что конечный прогноз у него получился совсем другим. Это расхождение было вызвано разницей в исходных значениях, не предвышающей одной тысячной! Это был не баг, нет. Это была фича хаотических систем. Он поделился своим открытием в статье с названием «Вызывает ли взмах крыльев бабочки в Бразилии торнадо в Техасе?» Так в науку вошёл эффект бабочки.
Лоренц удачно назвал феномен. Достаточно взглянуть на траектории его упрощённых моделей, которыми он показывал стремление системы прийти к одному из аттракторов в зависимости от начальных условий.
Хаотической системой является движение планет вокруг Солнца. В конце девятнадцатого века Ковалевская вместе с Миттаг-Лефлером поставили гравитационную задачу N тел, за решение которой давалась премия в 2500 шведских крон. Ставился вопрос о стабильности орбит в Солнечной системе. Через три года проблему удалось блестяще решить Анри Пуанкаре на примере трёх тел. Премию он получил, но очень скоро нашёл у себя ошибку и впоследствии доказал, что систему дифференциальных уравнений для движения трёх тел невозможно свести к интегрируемой. Что уж говорить о большем количестве Мы не можем точно рассчитать движение планет Солнечной системы в течение произвольного промежутка времени. Точка.
Итак, даже теоретически мы не можем смотреть достаточно далеко в будущее. Поэтому следует сторониться тех, кто говорят, что совершенно точно знают, что случится. Не знают. Не могут знать.
Кто не верил в дурные пророчества,
В снег не лег ни на миг отдохнуть,
Тем наградою за одиночество
Должен встретиться кто-нибудь.
В эпилоге автор говорит нам, что если есть хоть бы один урок, который можно извлечь для себя из его книги, то это необходимость делать выводы из своих несбывшихся планов и учиться на своих ошибках. Негусто.
Как по мне – получилось эклектично. Какой-то салат из очевидных фактов, вырезок из прессы и пространных поучений. Желание автора в книге на математическую тему обойтись без формул раздуло её аж до четырёх сотен страниц. Хорошо тем, у кого есть время на их усвоение, остальным придётся, чертыхаясь, перепрыгивать абзацы и пролистывать совершенно тривиальные вещи.
Что-то новое можно для себя почерпнуть, но, скорее, фрагментарно. И бессистемно. Но излагает наш автор весьма понятно и увлекательно. Что есть, то есть. Уважаю.
Эффект бабочки и Хаос Вселенной
1893 г., Киото, Япония
Молодой адвокат Генри Стимсон и его супруга Мэйбл Уайт проводят медовый месяц в Киото. Молодожены восхищены колоритом восточного города и его древней историей. Это путешествие запоминается им обоим на всю жизнь.
11 мая 1945 г., Лос-Аламос, США
Специальный комитет армии США формирует список приоритетных целей для атомной бомбардировки. Первую строчку в нем занимает Киото как крупнейший индустриальный центр страны. Ссылаясь на высокую культурную значимость города, министр обороны США Генри Стимсон лично вычеркивает его из списка. В итоге, Хиросима становится первоочередной целью американских войск; следом за ней угроза нависает над городом Кокура...