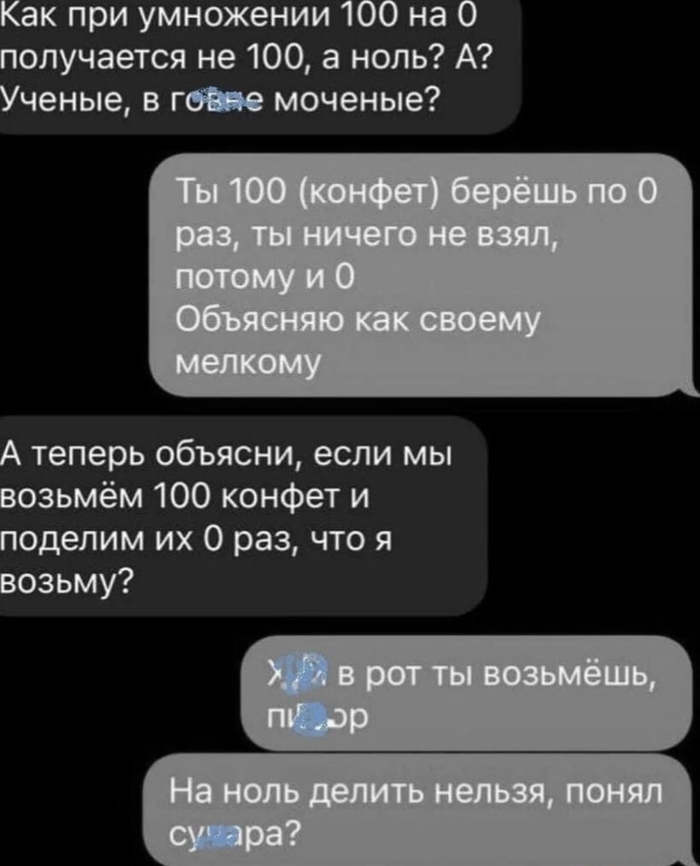
Делить на ноль
Сколько уже можно этот бред с умножением или делением на ноль...
0 это цифра а не число, на цифру нельзя ни умножать ни делить. Вы можете разделить яблоко на грушу? Или умножить мышь на кота? Да и сложить вы их не сможете.
0 * 5 = 0 + 0 + 0 + 0 + 0
5 * 0 =
ничему не равно, ни нулю, ни груше, ни вселенной. Если взять 5 нулей, будет 00000 а не 0
0 это цифра. Из цифр образуются числа. Из букв образуются слова. Мы не буквами говорим а словами, мы числа считаем а не цифры.