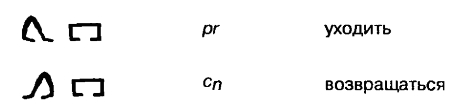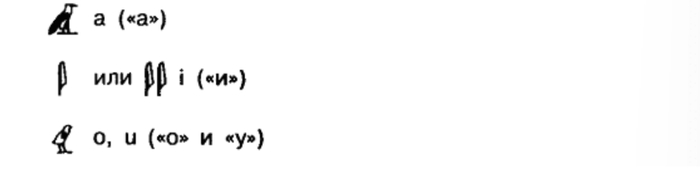Лига образования
Про псов и львов
Было в шумерском такое слово - 𒌨 [ur], которое означало что-то вроде "зверь" или "дичь".
Так вот, в сочетании с 𒂠 [gir] ("местный, домашний") получалось слово UR.GIR, что означало "собака".
А в сочетании с 𒈤 [mah] ("большой") это был UR.MAH, то есть "лев".
Так что для шумера в чём разница между псом и львом? Один тут возле дома болтается, а другой большой.
[пруф]
Древнеегипетский язык без проклятий и регистрации. Часть первая: письменность
Возможно, прочитав название статьи, кто-нибудь испытает легкий приступ благоговения: вот-вот приоткроется завеса тайны. Во всяком случае, с детства мы впитываем ощущение загадочности, которое окутывает всё, что связано с Древним Египтом.
Однако мало того, что древнеегипетский язык уже лет двести как расшифрован, он ещё и очень простой. Единственная тайна, и то не самая неразрешимая, - это произношение, но подступиться к нему достаточно близко нам позволяет прямой потомок египетского языка - коптский (скажем, разница между коптским и египетским примерно такая же как между итальянским и латынью, то есть она есть, и как именно звучала настоящая латынь, никто не знает, но и такого гигантского ореола таинственности вокруг латыни нет).
При этом египетский на порядок проще, чем латынь. Здесь не будет ни времён, ни спряжений, ни склонений. Серьёзно. Возможно, это самый простой язык из всех, которые вы когда-либо изучали.
Ещё один момент, который нужно понять сразу: на египетском языке говорили более трёх тысяч лет. За то же самое время праиндоевропейский успел разложиться на десяток отдельных языков. Поэтому рассматривается обычно самый классический вариант (он называется среднеегипетским), на котором говорили в конце III - первой половине II тыс. до н.э. - то есть спустя пару веков после Хеопса, за пару веков до Эхнатона и Нефертити и за полторы тысячи лет до Клеопатры.
Этот период удобен тем, что он большой, богат на надписи, а также одинаково близок и к более древнему варианту языка, и к более новому. Это как если через пару тысяч лет лингвисты будут изучать древнерусский, чтобы получить примерное представление одновременно о нём, о праславянском и о русском языке XXI века.
А есть ли родственники?
Да, египетский язык, в отличие от того же шумерского, не возник внезапно из ниоткуда. Относится он к семито-хамитским языкам, где одну группу составляют семитские (аккадский, арамейский, иврит, арабский и т.д.), другую - кушитские (это языки северо-востока Африки, например, галла или сомали), третью - ливийско-берберские (например, туарегский, нумидийский, ливийский), а в четвёртой группе гордо и отдельно восседает египетский.
Письменность
Письменность у египтян появилась примерно тогда же, когда клинопись в Месопотамии (в конце IV тыс. до н.э.), поэтому сложно сказать, кто был первым. В обоих случаях развитие письменных знаков шло от картинок, точно передающих смысл (пиктограмм), до символов, передающих звук. Разница только в том, что шумеры в Месопотамии ушли дальше от исходных изображений, а египтяне продолжали писать символами, напоминавшими своё первоначальное значение. Вероятно, египтяне намеренно сохраняли вид своих иероглифов, поскольку считали их священным даром свыше, с которым нужно было обращаться бережно. Таким образом за три тысячи лет внешний вид иероглифов практически не изменился.
Само слово "иероглиф" - греческое, состоит из частей ἱερός [hierós] ("священный") и γλῠφή [glyphḗ] ("резьба"). Это примерная калька с египетского их названия "mdw-nṯr" ("слово бога").
Единственное изменение в иероглифах произошло в самом начале, когда к картинкам стали добавлять другие картинки - детерминативы. Дело в том, что по мере развития письменности расширялся спектр возможных значений каждого изображения, и тогда для того, чтобы облегчить понимания, к ним стали добавлять подсказки. Дальше на протяжении нескольких тысяч лет не происходило ничего. Всего получилось около семисот символов, из которых активно использовали меньше двухсот.
Писали египтяне и справа налево, и слева направо, и сверху вниз, как придётся, в этом плане нравы у них были довольно свободные. Определить направление несложно: картинки "смотрят" туда, откуда надо читать.
Зато сложность есть в том, что гласные обычно не писали, например, глагол "говорить", который, скорее всего, звучал как "джед", писали двумя буквами: "дж" и "д". Современникам произношение было очевидно, как если бы мы сейчас записали слово "современник" в виде "сврмннк". А вот потомки могли бы условно произносить его "севременнек", и это было бы хотя и понятно, но неточно.
Другая сложность заключается в наличии "лишних" на наш взгляд знаков. Дело в том, что хоть египтяне могли бы обойтись набором из тридцати-сорока иероглифов, обозначавших конкретные звуки (фонограмм), они пользовались также идеограммами - символами, обозначавшими целые слова и понятия, а также иероглифами, передававшими сразу два или три звука (и это были абсолютно те же звуки, которые можно было передать отдельными знаками). Что ж, не нам их судить, такая избыточность была связана как раз с тем, что реформировать письменность считалось богопротивным делом.
Иероглифы
Звуки, передаваемые символами, получались, как правило, из слов, которые изначально обозначало изображение: брали первый звук или первый слог. Например:
Когда символ нужно было понимать как целое слово, к нему часто добавляли детерминатив. Например, изображение идущих ног передавало значение движения. В сочетании с символом дома этот детерминатив указывал на то, что речь о движении, плюс задавал направление, к дому или от дома:
Кроме того, детерминативы помогали различать слова-омографы (которые писались одинаково). Возможно, вслух они произносились по-разному, но на письме, без гласных, это было не отразить. Например, слова "старик" и "почитание" выглядели одинаково (мы не знаем, только на письме, или вслух тоже). Чтобы их различать, в первом случае ставили детерминатив "старик", а во втором - "поклонение":
Были и намного более запущенные случаи, например, у слова "wn" был целый набор совершенно разных значений:
Самый простой детерминатив - просто черточка - указывал на то, что слово нужно понимать целиком, а не только его первый звук:
Для некоторых гласных всё-таки были отдельные знаки, но обычно они использовались для имён:
Знаки, которые передавали сразу несколько звуков, почти всегда одновременно могли означать и отдельное слово (откуда они и происходили):
Вот такие были основные принципы написания, в следующий раз продолжим и перейдём к морфологии и синтаксису :)
Источник:
Боневиц "Иероглифы для начинающих"
Сооружение построек с целью нанесения ущерба соседям...
...именно так толкует словарь немецкое слово "Neidbau". Существовало оно уже как минимум в XV веке, сложившись из "Neid" ("зависть") и "Bau" ("строение").
То есть, если вам на участке, в целом, не нужен сарайчик именно на этом месте, но вы его строите ради того, чтобы на грядку соседа не попадало солнышко, то вы делаете Neidbau.
В английском это можно выразить как "spite house" ("дом назло"), в Индонезийском - "rumah dendam" ("дом мести"), в хинди - द्वेष घर [dveṣ ghar] ("дом ненависти"). А в русском что-то такое есть?
Российские школьники завоевали 3 золотые и 1 серебряную медали на Международной олимпиаде по химии имени Абу Райхана Бируни
Соревнование (ARBIChO 2025) проходило для участников из 16 стран в два тура. Практический состоял из двух задач, на выполнение каждой отводилось 2 часа 10 минут. Теоретический включал восемь заданий, рассчитанных на 5 часов.
Российская команда завоевала 4 медали:
Арсений Сысоев, Москва - золото
Владимир Руренко, Москва -серебро
Азамат Шарафиев, Казань - золото
Саид Нургаянов, Казань - золото
Руководитель - Василий Краснобров, методист Центра педагогического мастерства Москвы.
Ребята участвовали в соревновании в рамках подготовки к Международной химической олимпиаде (IChO), так как формат заданий и система оценивания были максимально приближены.
Get on VS Get in: как выбрать правильный глагол для каждого транспорта в английском
Я Настя, репетитор по английскому, и в этой статье мы с вами разберемся какие глаголы идут к различным видам транспорта. В конце - бонус, источник, где можно смотреть какие слова в английском можно сочетать друг с другом, а какие нет.
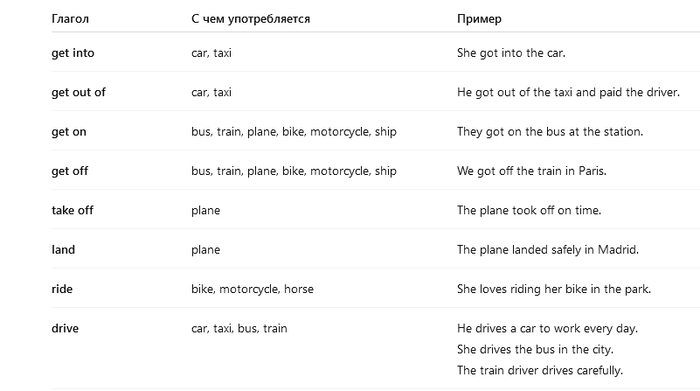
Таблица глаголов и видов транспорта
Вот, в принципе, и вся информация. Осталось только ее выучить (об одном из способов, как сделать это без особых усилий буду рассказывать в следующей статье).
Интересные нюансы
get in/into VS get on
Get in - мы используем, когда садимся в транспортное средство, в котором мы не можем, например, встать и пройтись. Машина, такси и т.д.
Get on - наоборот. Мы можем встать и пройтись в автобусе или поезде, однако помните, что это может быть небезопасно.
get out of VS get off
Работают по такой же схеме. Запоминайте в парах:
get in - get out of
get on - get off
ride
Когда ты сидишь сверху на чем-то - на лошади, велосипеде, мотоцикле.
catch
Успеть сесть на автобус или другой вид транспорта.
Бонус
Даю вам ссылку на словарь, в котором вы можете проверять сочетаемость слов. Например, вводите нужное существительное и смотрите - с какими глаголами или прилагательными оно может употребляться.
Кстати, а как сказать - "Я езжу на работу на автобусе"? 🤔 - Пишите ваши варианты в комментариях.
P.S. Если ты хочешь наслаждаться своим путем, изучать английский эффективно и с интересом, опираясь на свои ценности и увлечения – то приходи в мой блог. Там я делюсь своими мыслями про изучение английского, рассказываю про культуру и искусство Азии, а также делюсь книжными подборками и мотивирую быть добрее и нежнее к себе.
Страшное слово «профориентация»
Когда читаешь книги и журналы о жизни школьников в конце XIX – начале XX века, за голову схватиться можно. Тут вам и «приходские», и «внучки́ позорные», и «серые», и «чёрные». Открываем детский журнал «Галчонок» издания 1913 года и читаем на первой же странице:
«Невдали от Петербурга
Реалист весёлый Шурка
Жил на даче, в лес ходил,
Бил ворон, плотву удил…»
Кто такой этот самый «реалист»? Чем он отличается от гимназиста? Почему в книге «Швамбрания» Льва Кассиля враждовали (даже уже объединённые в один класс единой советской школы) бывшие гимназисты и бывшие «внучки́», то есть ученики высшего начального училища?
А ведь были ещё и прогимназии (и соответственно ученики прогимназий «прохоры» и «прошки»), и кадеты, и юнкера, и всякие «Разумовские училища» (читали «Храбрых беглецов» писателя Куприна?). В общем, нерабериха. А всё почему?
В переводе на обычный русский язык слово «профориентация» должно означать примерно следующее: «кем ты хочешь быть, когда вырастешь?», «какие взрослые работа и профессия тебя интересуют?». У школьников на этот счёт обычно в голове самая настоящая чехарда. (И это замечательно; хуже – когда пустота...)
Но человек живёт не сам по себе, а внутри огромного общества, и то, чем он занимается, определяется не только его личными желаниями и интересами, но и запросами того самого общества. А в обществе есть такое сложное понятие – «рынок труда», «структура занятости». Скажем (условно), чтобы отремонтировать лопнувший водопровод и вернуть людям в микрорайон подачу холодной и горячей воды, нам нужно десять рабочих, два шофёра, один экскаваторщик, один крановщик и один бригадир, который всеми этими людьми руководит. Всего пятнадцать человек. А если нам вместо них предложат пятерых блогеров, пятерых юристов и пятерых программистов? Вроде тоже пятнадцать человек – только водопровод они не починят!
Вот для «регулирования будущего рынка труда» в царской России и существовала очень сложная и многоуровневая система образования. Цель такой системы была довольно очевидна и проста – чтобы «на выпуске» получались именно те специалисты, которые нужны стране, и именно в нужном количестве – а не больше и не меньше необходимого.
Итак, гимназисты и «реалисты» – в чём разница между гимназией и реальным училищем? У гимназистов форма – серая с синим, у «реалистов» – чёрная с жёлтым, это понятно. Но единственная ли это разница? Нет. Смотрите: в гимназии химию, рисование и черчение вообще не преподавали. Не было там таких уроков! Зато иностранных языков было сразу целых четыре – латинский, греческий, немецкий и французский. А вот в реальном училище дети химию, черчение и рисование учили, а латинский и греческий языки – нет. И курс физики у них был более сложный и глубокий, чем в гимназии!
Идём дальше: школьник, который окончил гимназию (гимназист), имел право поступать в любой университет – прежде всего на философский, историко-филологический и юридический факультеты. А вот «реалисты» такого права вообще не имели! Выпускники реальных училищ могли поступать только в технические (политехнические) и коммерческие (торговые) институты.
Позже, правда, им дали право поступать и в университеты тоже – но только на физико-математический или медицинский факультеты. А, скажем, на юридический – ни-ни!
А ещё были так называемые «внучки́», то есть ученики высших начальных училищ, и «прошки», то есть ученики прогимназий. Программа в таких школах была легче и короче, чем у реальных училищ или гимназий, а выпускники могли поступать в учительские семинарии (то есть получить профессию учителя начальной школы), технические училища или юнкерские (военные) училища – но не в институты и не в университеты. Впрочем, чисто теоретически никто не мешал перевести ученика в реальное училище или гимназию – но нужно было выдержать очень сложный экзамен, и деньги за обучение платились совершенно другие. Скажем, высшее начальное училище стоило родителям ученика примерно десять рублей в год, а гимназия – пятьдесят рублей в год! Чувствуете разницу?
Короче говоря, чтобы стать в итоге адвокатом и «юристом-богачом», в те годы нужно было начинать «решать вопрос» в возрасте… девяти-десяти лет! Потому что юридический факультет – это сто процентов гимназия, то есть самая дорогая оплата, самые жёсткие требования, да плюс ещё и дорогостоящее домашнее начальное обучение.
Уже начинаете догадываться, для чего правительству России нужно было такой сложный огород с разными школами городить? Растущая империя прежде всего остро нуждалась в грамотных технических специалистах – военных, инженерах, строителях, механиках, железнодорожниках. Она нуждалась в работниках торговли и логистики, в школьных учителях (для начальных школ и тех самых технических/коммерческих училищ). А вот «гуманитарии» типа философов, историков, языковедов, юристов (современных социологов, психологов и политологов тогда ещё не изобрели) ей требовались в намного меньших количествах!
Само собой, люди (те же самые родители детей) всеми силами такой системе старались противостоять – ведь всем хочется для своих детей самой лучшей карьеры, самой престижной и «непыльной» работы, ну и плюс самого качественного образования! А в гимназиях, при всей их дороговизне и тяжести обучения, учителя были самые лучшие. Родители употребляли все возможные силы, чтобы отдать любимое дитя именно в гимназию – но часто просто «не тянули» ни по деньгам, ни по силам.
Одна из самых часто встречающихся в русской литературе «школьных» тем тех лет – вылет из гимназии. Вспомните рассказ Чехова «Случай с классиком» – четвероклассник Ваня Оттепелев «режется» на экзамене по греческому, и его мама плачет…
«– Нет, не ты, а я у тебя несчастная, подлый мальчишка! Я у тебя несчастная! Щепку ты из меня сделал, ирод, мучитель, злое моё произволение! Плачу за тебя, за дрянь этакую непутящую, спину гну, мучаюсь и, можно сказать, страдаю, а какое от тебя внимание? Как ты учишься?
А тётя вступается:
– Чего же ты его ругаешь? – набросилась на неё тётя, нервно стаскивая со своей головки платочек кофейного цвета. – Нешто он виноват? Ты виноватая! Ты! Ну, с какой стати ты его в эту гимназию отдала? Что ты за дворянка такая? В дворяне лезете? А-а-а-а… Как же, беспременно, так вот вас и сделают дворянами! А было бы вот, как я говорила, по торговой бы части! И себя ты замучила, и мальчишку замучила учёностью этой, чтоб ей пусто было. Худенький, кашляет… погляди: тринадцать лет ему, а вид у него, точно у десятилетнего…»
В финале рассказа несчастного Ваню наказывают ремнём и… «отдают по торговой части», то есть – в намного более дешёвое и лёгкое по программе (вообще без изучения не то что греческого, а любых иностранных языков!) коммерческое училище.
Можно вспомнить и «Золотого телёнка» Ильфа и Петрова, а именно Васисуалия Лоханкина:
«– Сермяжная? – задумчиво повторил Бендер. – Она же посконная, домотканая и кондовая? Так, так. В общем, скажите, из какого класса гимназии вас вытурили за неуспешность? Из шестого?
– Из пятого, – ответил Лоханкин.
– Золотой класс! Значит, до «Физики» Краевича вы не дошли? И с тех пор вели исключительно интеллектуальный образ жизни? Впрочем, мне всё равно…»
Можно вспомнить и «Серебряный герб» Корнея Чуковского – будущий знаменитый историк литературы, критик, переводчик и детский поэт, как и Лоханкин, был выгнан из пятого класса гимназии. В повести, правда, он уверяет, что его отчислили по так называемому «закону о кухаркиных детях», то есть как ребёнка бедных родителей, но тут Корней Иванович лукавит – циркуляр «о кухаркиных детях» был издан за пять лет до того, как Коля Корнейчуков в гимназию поступил, и выгнали его не за бедность, а за «малоуспешность в науках» и «вредное влияние на учащихся».
После революции всю эту сложную и громоздкую систему с «разделением школьников на разные сорта с самых малых лет» отменили, введя бесплатную «единую школу». С одной стороны, это было справедливо – детей больше не делили на «первосортных» гимназистов-гуманитариев, «второсортных» «реалистов»-инженеров, «третьесортных» «внучков» и так далее. С другой – но как же быть с тем самым «рынком труда», с его запросами? Довольно быстро советское правительство решило этот вопрос по-своему радикально: окончив единую школу, можно было поступать (или не поступать) в абсолютно любой вуз, только вот работать надо было совсем не там, где ты хочешь, а «куда пошлют» – то есть ввели обязательное распределение выпускников.
Сейчас и среднее, и высшее образование в России единые – с равными правами и возможностями для всех учеников/ студентов. И это хорошо. И обязательного распределения выпускников сейчас тоже нет – и это, наверное, тоже больше хорошо, чем плохо. Хотя (честно скажем) не все с этим согласны. И прежде всего – то самое государство, тот самый бизнес, промышленность и так далее. Потому что слишком часто возникают «перекосы» – скажем, в год выпуска автора данного текста программистов (ну модная тогда была профессия!) понавыпускали столько, что работу по специальности найти было очень трудно, если вообще возможно.
Потом такая же ситуация была с «модными» профессиями юристов, экономистов и бухгалтеров – впоследствии на каких только работах и должностях не оказывались «лишние» финансисты и адвокаты! Однако вмешательство государства в такие вопросы (скажем, путём введения того самого «узкоспециализированного образования с самой начальной школы», как в царские времена) упирается в абсолютное незнание того, какие же именно профессии будут наиболее востребованы к концу полного цикла обучения, то есть через десять-пятнадцать лет.
Так что пока проблема «у меня растут года, будет мне семнадцать / где работать мне тогда, чем заниматься?» как была неразрешимой «по справедливости», так и остаётся. А вам лично какая система нравится больше?
Статья из журнала «Лучик» №9/2024
Наш Телеграм-канал: t.me/luchik_magazine
Слова по теме “Food”
Каждую субботу я веду бесплатный разговорный клуб английского для всех желающих. Можно слушать и говорить на любом уровне, как получается, потому что все вопросы на клубе я дублирую текстом.