Продолжение поста «Равновесие Нэша и дилемма заключенного: как математика связана с развитием человеческой цивилизации?»3
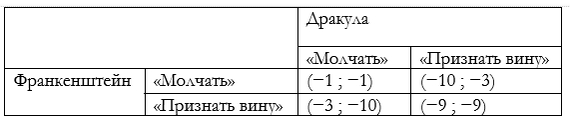
Равновесие Нэша - это рациональная математическая концепция, которая на первый взгляд кажется универсальным решением для построения гармоничных социальных систем. Однако, как подчеркивают участники дискуссии в комментариях к исходному посту, реальная жизнь вносит свои коррективы. Именно асоциальные элементы и психопатические (предельно эгоистические) стратегии могут нарушать любые попытки стабилизировать общество, если не предусмотрены механизмы их выявления и устранения.
Как пишет @Stellbard, «всегда будут асоциальные личности, которые при любой коммуникации забьют на договоренности» [#comment_334168427]. Это подчеркивает, что даже в кооперативной системе достаточно одного индивидуума, действующего против интересов группы, чтобы создать эффект домино. Именно это и ведет к эскалации насилия, дестабилизации и разрушению доверия внутри системы. Пикабушник @BozZiLLA добавляет: «Капитализмом движет не инновации и благополучие человечества, а страх потерять имущество и жажда прибыли» [#comment_334109297]. Это усиливает понимание необходимости контроля и регулирования эгоистичных стратегий.
Для решения этой проблемы на ум приходят два подхода:
1) идентификация и исправление/изоляция деструктивных элементов. Современные технологии (искусственный интеллект и нейросети) могут помочь выявлять манипуляторов и лиц с психопатическими наклонностями на ранних этапах.
2) образование и воспитание. Увеличение уровня знаний о теории игр, истории, политэкономии и кибернетике может уменьшить вероятность появления деструктивных стратегий. Однако, как отмечает @Pauluzzz, не все люди от природы склонны к обучению и пониманию сложных систем [#comment_334299419]. Я в комментариях предложил рассматривать социальный рейтинг как элемент воспитания, где корреляция денег и общественной пользы могла бы мотивировать людей действовать во благо общества [#comment_334111446].
Психопатические стратегии не раз проявляли себя в истории. Вот некоторые примеры, предложенные участниками обсуждения:
1) Колонизация Америки - конкистадоры использовали доверие коренных народов, чтобы затем манипулировать ими и эксплуатировать их ресурсы [#comment_334196637].
2) Манипуляции финансовых рынков в начале XX века, закончившиеся кризисом 1929 года - крупные игроки манипулировали доверием инвесторов, накачивая активы фиктивной стоимостью, чтобы потом обогатиться, обрушив рынок [#comment_334228121].
3) Вторая мировая война - нацисты под угрозой глобальной войны в начале довольно долго решали свои задачи, постепенно получая все больше ресурсов и влияния до начала столкновения [#comment_334218061].
4) Развал СССР - лидеры республик и партийные функционеры, декларируя приверженность общим целям, действовали в своих интересах, манипулируя массовым сознанием [#comment_334196637].
5) Кризис доткомов - создание фиктивной стоимости активов и манипуляции доверием инвесторов для извлечения максимальной выгоды [#comment_334218061].
Эти примеры показывают, что кооперативные системы, стремящиеся к равновесию Нэша, с высокой степенью доверия могут стать уязвимыми к действиям «психопатических игроков».
Возможно использовать возможности нейросетей и цифровизации для раннего выявления манипуляций и подрыва общественной ценности. Искусственный интеллект способен анализировать сложные паттерны поведения и сигнализировать о рисках. Например, нейросети могут быть полезны для диагностики психопатии и предотвращения деструктивных стратегий, основанных на манипуляции доверием.
Однако возникают вопросы:
1) Как гарантировать, что эти технологии не будут использоваться самими психопатами?
2) Как сбалансировать права личности и безопасность общества?
Многие участники дискуссии считают, что ключевую роль в построении устойчивой системы играет образование. Но, как замечает @Pauluzzz, невозможно добиться одинаково высокого уровня интеллекта у всех людей [#comment_334312109]. Тем не менее, я утверждаю, что интеллект можно развивать, приводя примеры обучения подопытных животных и собственного опыта, где мотивация и доступное объяснение помогли преодолеть трудности в обучении [#comment_334305180]. @BozZiLLA указывает, что в условиях коммунистической идеологии, несмотря на её антирелигиозный настрой, воспитывалась духовность, тогда как либеральная идеология капитализма часто фокусируется на материальных ценностях [#comment_334109297].
Еще один важный аспект - незамкнутость государств. В глобальном мире интересы отдельных групп могут идти вразрез с интересами государства. Например, перенос производств в страны с более низкими издержками труда подрывает экономику родной страны [#comment_334288664]. Решением здесь может стать кооперация на глобальном уровне (многополярный мир) и создание равновесия Нэша между государствами [#comment_334297651].
Наконец, обсуждение затронуло вопрос смысла существования человечества. @Pauluzzz скептически относится к идее космической экспансии и считает, что научное познание вряд ли станет универсальным смыслом для большинства людей [#comment_334299419]. Я обратил внимание на те же нейросети как на инструмент, способный компенсировать ограниченность человеческой жизни и способствовать достижению глобальных целей [#comment_334305180].
Вывод
Для достижения устойчивости в равновесном по Нэшу (многополярном) обществе необходимо учитывать:
1) Использование технологий для мониторинга и предотвращения манипуляций.
2) Раннее выявление и исправление/изоляцию деструктивных элементов.
3) Повышение уровня образованности и научности.
4) Кооперацию на глобальном уровне (многополярный мир) для создания равновесия интересов.
Какие еще подходы вы можете предложить, чтобы человечество смогло минимизировать влияние психопатических/эгоистических стратегий и направить развитие цивилизации в русло прогресса и гармонии?
P.S. В дебатах «Кооперативный капитализм vs Технологический коммунизм» проголосовало 76 человек, из них кооперативный капитализм выбрало 25%, за технологический коммунизм проголосовало 75%.