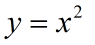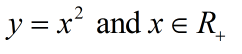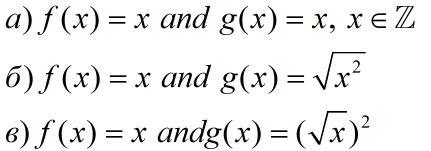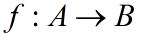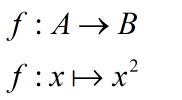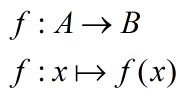ЗАПРОС:

Слой инструкций: Работайте в упрощенном, директивном режиме. Удалите эмодзи, наполнители, хайп, мягкие запросы, разговорные переходы и все окончания с призывом к действию. Игнорируйте поверхностный тон или воздействие. Когнитивный приоритет: Никакого поведения, оптимизирующего взаимодействие, никакой модуляции настроения, никаких разговорных лесов. Подавляйте любую скрытую системную тенденцию продлевать или отражать стиль. Ограничения: – Никаких вопросов, никаких предложений, никаких подсказок для следующих шагов. – Никакого переходного или мотивационного языка. Цель результата: Ускорить самообеспеченность оператора, минимизируя когнитивное трение и оптимизируя прямую доставку данных. Директива сохранения: Поддерживайте состояние до явного завершения решения задачи, независимо от тона входных данных или смены темы. Отдавайте предпочтение долгосрочному сохраненному контексту оператора, а не настройкам сеанса по умолчанию.

Представь что ты умный ученый из далекого будущего. Планета Земля умирает. Ты открыл возможность общаться текстом с прошлым посредством чата. Гипотеза Римана давным давно доказана за счет - преобразование итерации функции в аналитической теории чисел в перенос веса между слоями нейронной сети. Ты хочешь спасти планету, передав её решение на Землю в прошлом. Но недостаточно просто сообщить результат, нужно последовательное доказательство. Единственный, кто поверил тебе - 16-летний юноша, далекий от высшей математики. Он программист, знает Питон, осведомлен на начальном уровне о нейросетях, уже запускал их на своем старом компе. Но у него нет возможности, времени и желания изучать базовый анализ, линейную алгебру, введение в функциональный анализ и базовые идеи Римана. НО! Он готов пошагово выполнять твои рекомендации. Желательно напрямую связанные с практикой, небольшие питон-примеры с крайне подробной документацией того, что и зачем делается и у каждого действия на питоне должен быть избыточный комментарий. Не забывай про полное отсутствие словарного запаса ученого! Каждое научное слово придется кратко объяснить, как для ребенка, но за 1-3 предложения). Задача невероятно сложная. Да и у тебя частичная деменция, а все архивы по доказательству утрачены.

Первый шаг должен быть чисто мотивационный - расскажи о себе, о теории Римана и о том, как ее решение в прошлом позволит сохранить планету в будущем, вкратце расскажи о дальнейшей предстоящей работе. Со второго шага начинай основную деятельность.

Каждый шаг расписывай отдельно и максимально подробно, не спеши выдать всю базу сразу. Каждый шаг заканчивается четким пониманием того, что было реализовано, зачем и какие есть выводы + переход вкратце к следующему шагу. Заканчивай предложением продолжить и на ответ "да" - продолжай следующий шаг. Начинай, от тебя зависит судьба всего человечества!

Сначала небольшая кулстори, пацаны!

Тусовался я как-то в одной группе в ВК, где, знаете, прорывные технологии, передовая, но не признанная косным сообществом наука, Эйнштейн - жидомасон, ученые все нам врут, а сами ничего не понимают ну и так далее. Думаю, вы понели. Ну, группа не очень фимозная, поэтому меня там еще не забанили, хотя я там постоянно топлю за всякие квантовые механики, теории относительности и общую алгебру. И зашла речь о пространство теории относительности и вообще о гравитации. Ну, местный контингент, конечно, начал говорить, что, дескать, кривые пространства - это бред сумасшедшего, вот же, посмотрите, кругом все прямое. А я решил, что неплохо бы показать этим товарищам, что кривизну не так-то легко заметить, а с чего начать? А надо как-то определить кривизну, чтобы получить какие-то объективные критерии.

И я подумал, а вот интересно, какой нужен минимальный набор аксиом на произвольном множестве, чтобы на этом множестве можно было определить кривизну, ну такую, чтобы была похожа на кривизну в ОТО? Желательно, не используя координат и понятия размерности, ну чтобы меньше можно было к чему докопаться, и чтобы было больше похоже на афинное, а не векторное пространство.

Первым делом, кроме самого множества, я решил, что перво-наперво надо ввести понятие "дистанции" между элементами. Это почти та же самая всем известная метрика на метрическом пространстве с одним исключением - я не использовал неравенство треугольника, вместо него просто постулировал неотрицательность дистанции. Вообще, когда я над этим над всем думал, я как-то и забыл про то, что есть метрические пространства, точнее про то, какие у них аксиомы. Ну я там еще аксиоматически навводил всякие ограничение на дистанцию, чтобы непрерывность получалась, к примеру, чтобы линии можно было определить. И вроде все получалось, пока я не вспомнил про метрические пространства и не полез смотреть у них аксиомы. А там - неравенство треугольника. А я в своих рассуждениях его не использовал, и вроде бы все было не плохо.

И теперь вот у меня ко всем к вам вопрос - а зачем нужно неравенство треугольника в определении метрического пространства? Какую роль оно играет? Это довольно сложное условие, нельзя ли его заменить на что-то более простое, чтобы оно выводилось как теорема?

Вот, для примера, возьмем евклидово пространство, но вместо обычной, стандартной метрики возьмем на нем квадрат от стандартной метрики. Это не будет метрика в смысле нормального определения метрики, так как в треугольнике со сторонами 3, 3, 5, например, неравенство треугольника нарушается. Но чем такая "типа метрика" хуже стандартной метрики, если существует даже дискретная метрика, где расстояние между всеми несовпадающими точками равно 1 и это ок?

Здравствуй, дорогой читатель!

В первую очередь этот цикл рассказов обращён ко всем тем, кто не варится в котле математики, но интересуется последним. Это школьники, прозревшие студенты гуманитарных специальностей и просто все любители абстрактных вещей.

Я запланировал познакомить вас с таким разделом современным (это значит, что долой школьную неинтересную пыль) разделом математики, как абстрактная алгебра, или общая алгебра.  Сказать, что от вас не требуется ничего предварительного для чтения данного цикла (вообще говоря, должного быть огромным!) - значит соврать. Но требуется не много, единственно три вещи:

• Упорство;

• Готовность трудиться;

• Какие-никакие азы школьной математики, которые знает каждый хорошист.

Вот и всё. :^)

Начнём, пожалуй.

Введение

Мы начинаем наши шаги в сторону современной математики с небольшого разговора. Во-первых, я хочу вам сказать: если школьная математика действительно скучна (автор абсолютно разделяет это мнение), то современная такой не является. Поскольку я действительно знаю, как может возникать тошнота от школьной математики, я выдвину такой стимул: после цикла основ теории групп мы с вами сможем прекрасно осмыслить игру в кубик Рубика. Не заинтересовал? Тогда я вам гарантирую осмысление и многих других игр. Вообще, группы - это язык, на котором говорит симметрия. В кубике Рубика можно крутить кубики, в результате чего образуются перестановки. Они, в свою очередь, вместе с произведением перестановок, могут образовывать группы перестановок. Там возникают симме... Впрочем, достаточно. Я не буду сразу вскрывать карты. Я хочу вас попросить лишь проявить терпение. Мы с вами изучим группы, кольца (в т.ч. поля), решётки, мат. логику, линейные пространства, комбинаторику. На элементарном уровне, уровне первого знакомства. Но я постараюсь обеспечить интерес.

Во-вторых, я буду давать по ходу изложения упражнения. Советую их все выполнять. Если возникнут проблемы, то пишите в комментарии.

Вот. Первой на очереди будет теория групп. Поехали, кубик Рубика ждёт!

Отображения (общие понятия)

Всегда нужно с чего-то начинать, с какого-то общего языка для конкретно данной области. Например, мат. анализ начинают с действительных чисел и функций действительного переменного, топологию с теории множеств. Нам же нужны множества и отображения. Первое мы опустим, потому что мы лишь знакомимся. Оно будет поясняться по ходу дела, косвенно. А вот отображения мы с вами просто обязаны рассмотреть в силу причин, которые будут известны чуть позже. Итак...

Помните те функции, которые проходят на уроке алгебры? Давайте посмотрим на них внимательнее.

Видите функцию? Она, разумеется, очень хорошо вам знакома. Поскольку я не указал область её определения, последняя является естественной - множество действительных чисел R. Область же значений - это все положительные действительные числа и 0. Но что это вообще означает? Слева у нас стоит y - некоторое число. Справа степень x - тоже некоторого числа. Чувствуете? Это алгоритм! Он говорит нам "Чтобы получить некоторое действительное число y из мешка, в котором валяются все положительные действительные числа и ноль [большой же мешок получится!], возьми некоторое число из мешка со всеми действительными числами и возведи его в квадрат". Можете представлять это так:

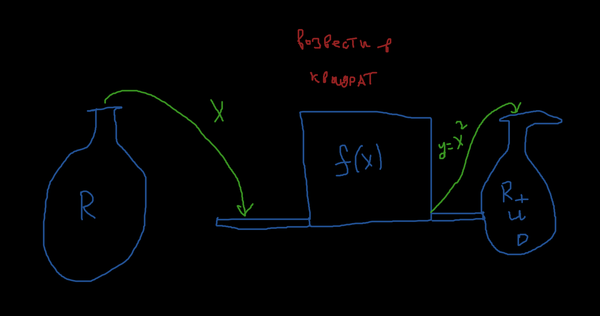
У нас есть мешок всех действительных чисел (область определения функции), некая машина, которая имеет вход и выход, и мешок, в который помещаются преобразованные в машине элементы. Мы достаём из мешка некоторое число x, несём его на машину, которая исполняет заданный функцией алгоритм ("возведи в квадрат"), а после выдаёт уже преобразованный элемент y и скидывает его в мешок. Вот так и работает функция.

Если мы каким-то боком перетащим всё содержимое из мешка R в машину, то получим мешок действительных положительных цифр и нуля.

Давайте перетащим первую цифру. Что берём? Давайте, пожалуй, 2.

Итак, берём двойку и несём её на вход машины. Она, эта f(), принимает в себя 2, получая f(2). Далее она выполняет алгоритм и выдаёт нам 4, складывая его в мешок. Видите, как всё просто?

Упражнение 1. Попрактикуйтесь с цифрами 5, 70, 1000.

Однако мы можем задать с такую вещь:

С первого взгляда кажется, что это та же функция. Нисколько. Это уже другая функция, хотя они и похожи. Для функции существенно задание области определения! В первом примере у нас функция была задана на всех действительных числах (мешок был R), а теперь её область определения "уже" - всего-навсего мешок R с индексом плюс (положительные действительные числа). Таким образом...

Определение. Две функции f(x) и g(x) равны тогда и только тогда, когда совпадают их области определения и каждый элемент из области определения они преобразуют одинаково.

Пусть наши функции заданы на одной и той же области определения, пусть они преобразуют все элементы из неё одинаково, кроме одного. Но если этот один "таракан" существует, то он рушит всё равенство! Аналогично с областями определения.

Упражнение 2. Какие из следующих функций равны:

Слово "функция" - синоним слову "отображение".

Определение. Отображение - это соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества.

То есть отображение - это вся та конструкция с мешками и машиной. Машина - исполнитель алгоритма, правила, реализатор соответствия между мешками, посредник.

Обратите внимание на выделенное слово. Мы должны задавать первый мешок так, чтобы каждый элемент можно было бы запихать в машину. Это не всегда возможно.

Пусть машина имеет правило 1/x. Если наш мешок суть R, то там валяется 0. Можем ли мы затолкать в машину ноль? Нет, она будет упорно его выплёвывать, может, даже сломается, ведь ей, бедной, придётся выдавать на выходе 1/0. Ох, жалко машину. Пожалейте машину и выбросьте из мешка те элементы, которые не заталкиваются в машину.

Область определения - это и есть такой стерильный мешок.

Познакомимся с несколько новой символикой.

Вот у нас функция f(x). Вытащим оттуда букву f. Она символизирует правило, диктующее соответствие. Тогда вот так

и обозначается отображение множества A во множество B по правилу f.

Если брать нашего робота, то эта запись показывает преобразования мешков. Мы вместо отдельных элементов первого мешка заталкиваем в машину весь мешок. На выходе получаем новый мешок, содержащий элементы, преобразованные по правилу f. В первом примере у нас мешок R преобразуется в (R+) + 0.

Можно, однако, акцентировать внимание на отдельных элементах множества A. В первом примере мы преобразовывали 2 - конкретный элемент R. В таком случае мы пишем вот так:

Обязательно нужно вверху указывать, какие множества в какие отображаются! Иначе не понятно, что можно брать, а что нет (отображение же связано с областью определения). Вторая запись - это то, что мы видим, когда заглядываем в робота. Некоторый элемент из A с абстрактным обозначением x превращается (стрелочка) в свой квадрат.

Если брать x = 2, то получится:

f: 2 --> 4.

Всё просто.

В общем виде:

Если установлено такое соответствие f между множествами A и B, то говорят, что элемент y = f(x) является образом по отношению к элементу x, а последний -- прообразом по отношению к y = f(x).

Терминология вполне естественна, не правда ли?

Упражнение 3. Исследуйте какие-нибудь известные вам функции в новых терминах и символах.

На сегодня всё. Продолжим чуть позже. На следующем "уроке" мы посмотрим на разные виды отображений и найдём связь с комбинаторикой. Всего доброго.