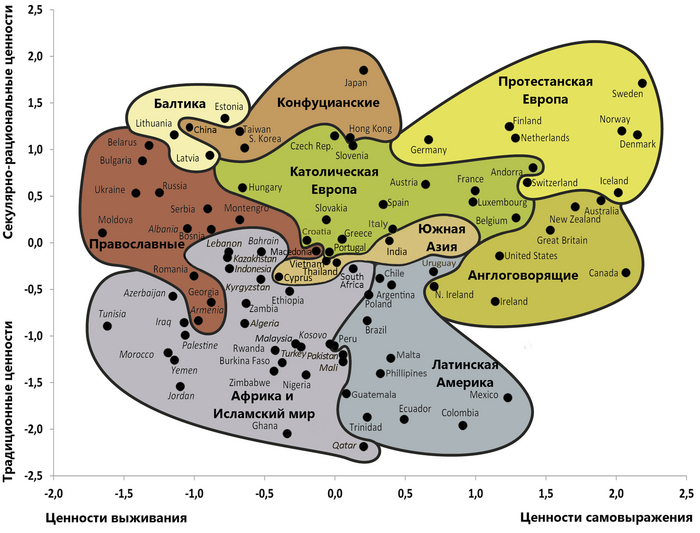
Эту диаграмму часто показывают политологи и социологи, однако есть у меня подозрение, что мало кто из них представляет, каким образом рассчитываются координаты каждой страны и что такое эти координаты. Как строятся такие карты лучше всего знают статистики, потому что делается это статистическим методом под названием "факторный анализ".
Все подробности построения диаграммы мне найти не удалось (это описано в книгах Инглхарта, а они не бесплатные). Однако того, что я нашел хватит для объяснения принципа.
Сразу оговорюсь, что бласти, выделенные на диаграмме (и их названия) не имеют никакого отношения к построению диаграммы. Это разделение было придумано совсем другим автором (Хантингтоном) и просто взято у него.
Исходные данные для этой карты - это 10 индикаторов. Каждый индикатор - цифра, полученная из ответов людей (респондентов) в ходе опросов. Вот список этих индикаторов:
1) Бог очень важен в жизни респондента.
2) Для ребенка важнее научиться послушанию и религиозной вере, чем самостоятельности и решительности.
3) Аборт никогда не может быть оправдан.
4) У респондента сильно развито чувство национальной гордости.
5) Респондент выступает за большее уважение к власти.
6) Респондент отдает предпочтение экономической и физической безопасности над самовыражением и качеством жизни.
7) Респондент описывает себя как не очень счастливого.
8) Гомосексуальность никогда не может быть оправдана.
9) Ответчик не подписал и не подпишет никакой петиции.
10) Вы должны быть очень осторожны, доверяя людям.
В методе факторного анализа мы предполагаем, что значения индикаторов определяются (коррелируют) небольшим числом скрытых факторов. Эти факторы мы не можем измерить напрямую (часто даже сложно понять их смысл).
В данном случае Инглхарт предположил, что для каждого респондента есть только два фактора, с которыми связаны значения всех десяти индикаторов. Причем первый фактор коррелирует только со значениями индикаторов 1-5, а второй - со значениями 6-10.
Затем, на основе этого предположения в факторном анализе "подгоняются" значения факторов так, чтобы они наилучшим образом коррелировали со "своими" индикаторами. Делается это специальными программами и методами.
Чтобы лучше понять проблему, представьте таблицу, где в строчках респонденты, а столбцы - значения индикаторов. Нам нужно к этой таблице добавить столбец цифр (фактор) так, чтобы он хорошо коррелировал со всеми столбцами ("предсказывал" значения столбцов).
Можно туда просто скопировать, например, значения первого столбца тогда наш фактор будет идеально коррелировать с ним. Однако с другими столбцами он будет плохо коррелировать. А задача состоит в том, чтобы подобрать значения фактора так, чтобы он "более-менее" коррелировал со всеми столбцами. Т.е. нужно сложить с какими-то коэффициентами значения всех столбцов, так, чтобы суммарная корреляция была наилучшей.
В результате "подгона" Инглхарту удалось подобрать значения первого фактора, так, что фактор объяснял (предсказывал) в целом 26% вариаций индикаторов 1-5 и значения второго фактора, так, что он объяснял 13% вариации индикаторов 6-10.
Я предполагаю, что вычислив факторы для всех респондентов автор просто усреднил значения по каждой стране и отобразили точками на диаграмме. Т.е. координаты - это два фактора, наличие которых предположил Инглхарт, а положение стран - их усредненные значения.
Обычно в таком типе анализа (подтверждающий факторный анализ) обязательно проводят тестирование гипотезы о том, что факторы коррелируют с индикаторами (что это не случайное совпадение). Т.е. все это подтверждается статистикой, а не просто является выдумкой автора.
А вот названия факторов и их интерпретация - это уже субъективное мнение автора. Инглхарт решил, что первый фактор (индексы 1-5) отображает ценности традиционные/рациональные, а второй (индексы 6-10) - ценности выживания/самовыражения.
Список индикаторов взят отсюда