Продолжение поста «Как искать жульничество в цифрах. Закон Бенфорда, или закон первой цифры»
Появился комментарий, в котором интересуются подробностями применения этого закона для обнаружения жульничества (спасибо @toyoroyo1 за вопрос).
Поэтому пишу продолжение.
Чтобы выявить подделку нам нужно пересчитать первые цифры в данных и сравнить с тем, что должно было бы получиться согласно закону Бенфорда. (То, что должно получится считается умножением количества чисел в наших данных, на частоты их появления по закону Бенфорда.)
Для примера я возьму данные "Корпоративные платежи коммунальной компании Западного побережья - 2010 г." (это все про США)
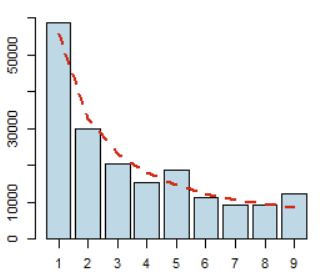
Вот что у них получается:
Красная линия - это что должно быть, столбики - что есть на самом деле. Видно, что есть различие, но это может быть и чисто случайное различие. Это как с игровым кубиком, у него вероятности цифр одинаковые, но если его подбросить 180 раз, то цифры не выпадут точно по 30 раз, будет отличие, которое можно объяснить случайностью.
Так же и тут. Весь вопрос в том, случайно ли отличие, что мы видим.
И тут нам поможет критерий x-квадрат.
Мы просто говорим - допустим это все случайно, посчитаем вероятность случайности при которой мы увидим такое отличие. (Суммарное отличие считается хитро, не буду писать)
В нашем примере получается вероятность меньше чем 10e-16 (десять в минус шестнадцатой степени) - то есть вообще никогда!
А это значит нарушен закон Бенфорда и с данными что-то не так, нужно смотреть подробнее.
Вот как-то так.
Звучит сложно, но в реальности я просто запустил Rstudio и набрал команды:
library(benford.analysis)
data(corporate.payment)
bfd.cp <- benford(corporate.payment$Amount, number.of.digits = 1)
bfd.cp
plot(bfd.cp)
Так и получил все графики и вероятности.