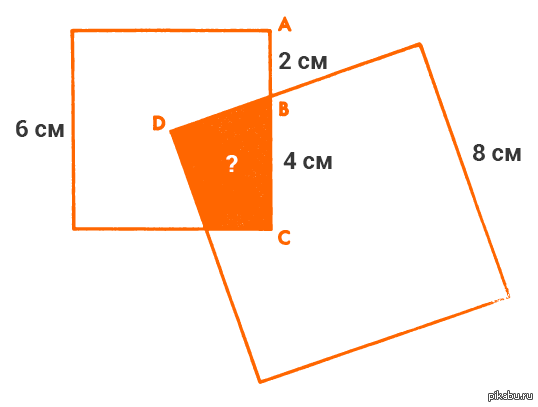
Задача
Эту логическую задачу придумал Мартин Гарднер еще в 1970-х. Илон Маск одно использовал ее во время интервью кандидатов на работу:
"Вы стоите на поверхности Земли. Вы прошли 1 километр на юг, затем 1 километр на запад, затем 1 километр на север. В итоге вы оказались там же, где и начинали. Перечислите всевозможные места, где вы могли бы находится в начале."
Подсказка: возможных мест больше, чем одно!
Математические досуги. Лента Мёбиуса.
Что такое "лента Мёбиуса", кто не знает, может погуглить сам, я же, владея лишь человеческим языком, опишу этот объект так - кольцо из плоской ленты, перекрученное внутри себя на полоборота
В детстве мне попалась в руки книга американского математика Мартина Гарднера "математические доуги", которую я, имея скорее гуманитарный склад ума, всё же с интересом читал. Там был описан интересный опыт разрезания этой ленты вдоль. Я решил сделать такую ленту и проверить, что получается
Сделал из широкой изоленты, разрезал
И получил, как и было описано - вдвое более длинную, дважды перекрученную ленту Мёбиуса!
И тут мой гуманитарный мозг осенила идея. А что получится, если её разрезать еще раз ?
Никаких причин откладывать у меня не было, и я это сделал.
Внимание, вопрос) У кого какие мысли, что у меня получилось?
Результат меня удивил, не скрою, ответ дам чуть позже)
Одна из задач Мартина Гарднера. Вроде бы похожих нет...
Наименьшее из чисел с числом стойкости, равным одному, — 10, для числа стойкости 2 это будет 25, самое маленькое число со стойкостью 3 — 39, если число стойкости равно 4, наименьшим числом для него будет 77. Каково наименьшее число с числом стойкости 5?
P.s. у меня получилось 679 - кто меньше?