Серия «Математика и всё»

Всем привет, мои злобные печенюги!
Пишу продолжение своему посту (все думают, что я слился, а я в бане парился, поэтому не смог ответить на ту теплоту, с которой зашёл первый пост).
Основная мысль - программисту без математики никак. И у меня здесь животрепещущий пример этому утверждению (ибо давненько не было программирования в группе про программирование).

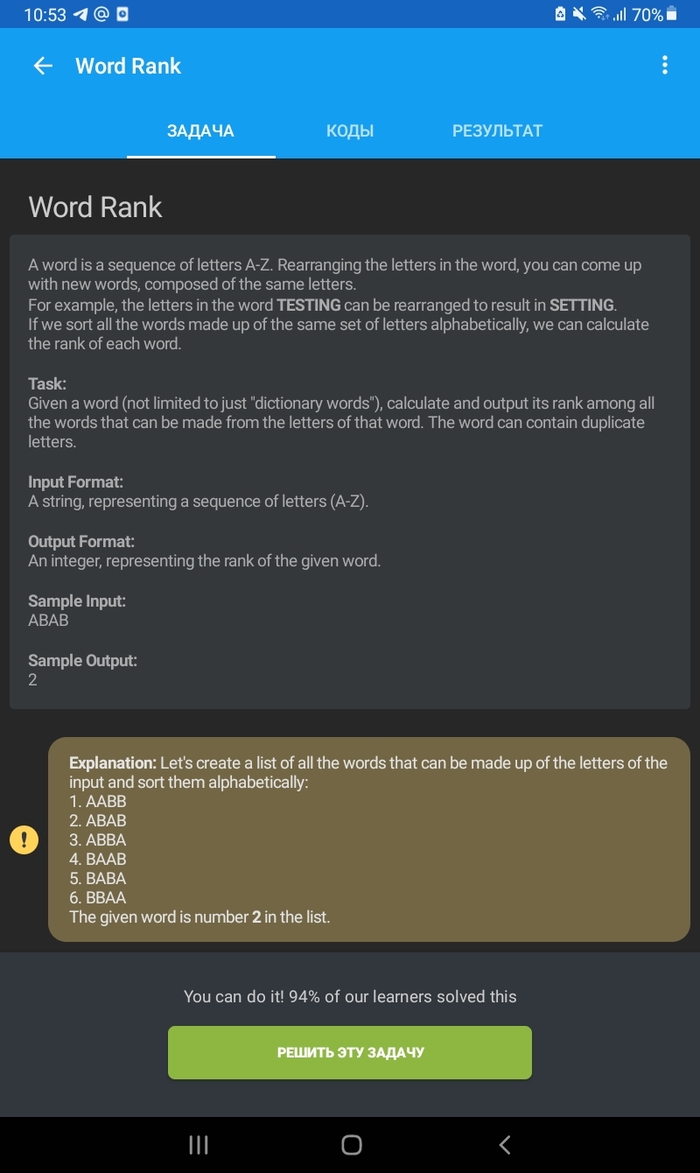
Сама задача

Это дополнительная задача с пометкой "сложная" из курса по Python программы Sololearn. От пользователя принимается слово. Необходимо указать его порядковый номер в ряду всех возможных комбинаций, составленных из букв этого слова. Комбинации при этом располагаются по возрастанию. Вот такая в принципе задача. У нас в армии говорят, что любую задачу можно выполнить: правильно, неправильно и по-армейски. И вот первое решение, без всяких математических знаний, как говорится, по-армейски. То есть как бы правильно, но...

Решение № 1: не математическое, армейское.

Само решение:
from collections import OrderedDict
slovo = input()
sinbol = list(slovo)
sinbol.sort()
azbuka = []
kod = ""
kol_simv = []
i = 0
while i <= (len(sinbol)-1):
if i == 0:
kod += "1"
kol_simv.append(1)
i += 1
azbuka.append(sinbol[0])
continue
if sinbol[i-1] == sinbol[i]:
kod += str(int(kod[len(kod)-1]))
kol_simv[len(kol_simv)-1] += 1
else:
kod += str(int(kod[len(kod)-1])+1)
kol_simv.append(1)
azbuka.append(sinbol[i])
i += 1
i = 1
tabl_index = []
minimum = ""
maximum = ""
while i <= len(slovo):
minimum += str(i)
i += 1
i = len(slovo)
while i >= 1:
maximum += str(i)
i -= 1
minimum = int(minimum)
minimum1 = minimum
maximum = int(maximum)
while minimum <= maximum:
for i in str(minimum1):
if not (str(minimum).count(i) == 1):
j = 0
while j <= len(str(minimum))-1:
if not (str(minimum1).count(str(minimum)[j]) == 1):
minimum += int("1"+("0"*(len(str(minimum))-j-1)))
j = ""
break
j += 1
if j == "":
break;
minimum += 1
break
if i == str(len(str(minimum))):
s = 0
t = 0
summ = 0
ebat = minimum
huy=""
#Работа тут!!! перебор строки и сравнение ее значений
#с нужным количеством симв
while s <= len(str(ebat))-1:
while t <= (len(kol_simv)-1):
#print(t+1)
summ += kol_simv[t]
if summ >= int((str(ebat))[s]):
#print("Заменю "+(str(ebat))[s]+" на "+str(t+1))
#ebat = str(ebat).replace((str(ebat))[s], (str(t+1)))
huy += str(t+1)
t = 0
summ = 0
break
#print("Смотрю симв "+(str(minimum))[s]+" должно быть "+str(t+1)+" в количестве "+str(kol_simv[t]))
t += 1
summ = 0
t = 0
s += 1
#ebat = int(ebat) - int("1"*len(ebat))
tabl_index.append(huy)
minimum += 1
print(huy)
tabl_index = list(OrderedDict.fromkeys(tabl_index))
ddd =""
for i in slovo:

ddd += str(azbuka.index(i)+1)
print(tabl_index.index(ddd)+1)

Коротко как все тут работает:
От пользователя принимается слово. Далее из букв этого слова составляются все возможные комбинации слов, повторы удаляются. В конце концов, в последовательности ищется слово пользователя, выводится его порядковый номер. Здесь есть кой-чего лишнего, но на скорость работы это критического влияния не оказывает.
Критическое влияние оказывает количество комбинаций и, как следствие, количество итераций. Программа быстро обрабатывает слова до 5 - 6 букв, а если их больше, то все. Компилятор для андроид Coding Python может провести вычисления, и они все верны, но сама обучающая программа пишет что-то вроде No output при попытке провести вычисления.
Словом, решение работает, но так, что ну его в пень. Предвижу заявления, что можно сразу сравнивать искомое слово с каждым новым и сразу сравнивать каждое новое сочетание с уже имеющимися, удаляя повторы. Отвечу - можно, но на быстродействие этот не окажет большого влияния, подумайте про слово "Югославия", оно в ряду 295.753-е...

Решение №2: математическое

# принимаем слово, сортируем буквы и кодируем (в строках 4 и 5 так и должно быть, иначе компилятор почему то сортирует обе переменные)
slovo = input()
slovo_poryadok = slovo
chislo_poryadok = slovo
chislo = slovo
chislo_zagotovka = slovo
slovarb = slovo
i = 0
chislo_poryadok = list(chislo_poryadok)
slovarb = list(slovarb)
for i in range(len(chislo_poryadok)):
chislo_poryadok[i] = 0
slovo = list(slovo)
slovo_poryadok = list(slovo_poryadok)
slovo_poryadok.sort()
i = 0
j = 0
for i in range(len(slovo_poryadok)):
if i == 0:
chislo_poryadok[i] = 1
slovarb[j] = slovo_poryadok[i]
else:
if slovo_poryadok[i-1] == slovo_poryadok[i]:
chislo_poryadok[i] = chislo_poryadok[i-1]
if slovo_poryadok[i-1] != slovo_poryadok[i]:
chislo_poryadok[i] = int(chislo_poryadok[i-1])+1
slovarb[j+1] = slovo_poryadok[i]
j += 1
del slovarb[j+1:]
# проводим математические расчёты (вычисляем общее количество комбинаций в зависимости от количества повторящихся букв)
k = 1
kol_komb = 1
while k <= (i+1):
kol_komb *= k
k += 1
for k in range(len(slovarb)):
n = 1
while n <= slovo_poryadok.count(slovarb[k]):
kol_komb /= n
n += 1
kol_komb = int(kol_komb)
# переводим слово в числовой код
chislo = list(chislo)
chislo_zagotovka = list(chislo_zagotovka)
for n in range(len(chislo)):
chislo[n] = slovarb.index(chislo[n]) + 1
chislo_zagotovka[n] = chislo[n]
#ищем положение слова в ряду
diapazon = kol_komb
otstup = 0
for i in range(len(chislo)):
for j in range(len(slovarb)):
if slovarb[j] < slovo[0]:
otstup += diapazon*(slovo.count(slovarb[j]))/len(slovo)
if j == len(slovarb)-1:
diapazon = diapazon/(len(slovo)/(slovo.count(slovo[0])))
del slovo[:1]

print(slovo, diapazon, otstup)
print(int(otstup)+int(diapazon))

Как это работает?
От пользователя принимается слово. Далее проводим математические вычисления, вычисляем общее количество комбинаций из указанных букв (учитывая, что буквы повторяются):

где n - это общее количество символов включая повторы, a с индексом b - количество повторений символов. Если всех символов по одному (как в слове "один"), то и формула превращается в одинокий факториал.
В конце всего ищем положения слова в ряду, используя количество комбинаций, количество символов. Определяющими величинами будут:
Otstup - при первой итерации равен нулю, по сути он и является искомым положением, находится эвристически, мы просто отбрасываем области, где заведомо указанного значения нет (а именно - комбинации (слова), начинающиеся с более "младшей" буквы).
Diapazon - при первой итерации равен общему количеству комбинаций (слов), показывает рассматриваемую область. По существу мы анализируем наше слово с первой буквы, отбрасывая все комбинации (слова), где первая буква - другая. Далее переходим ко второй букве и так до конца слова.
Количество комбинаций (слов), где есть нужная нам первая буква вычисляется по формуле:

где n - количество букв в слове, а с индексом 1 - количество повторений первой буквы слова.
Такое решение ввиду его скорости программа Sololearn приняла. Так что математика в программировании рулит, здравия желаю!

Пэ. Сэ.: Вентилятор раскрутил, жду отборного дерьма комментария. Вообще, когда решал задачу, была мысль, что наверно есть какие то библиотеки для работы с комбинациями или вовсе - что-то такое явное из базового программирования, что я проглядел...

В пору моей учебы в военном училище я немного увлекался математикой, поэтому в библиотеке читал много литературы по этому вопросу.

Однажды, мне попался в руки журнал "Вокруг света" (ни номера, ни года я вам не припомню). Там одно время была интересная рубрика про новые научные открытия. Статья, о которой мы говорим, рассуждали о кризисе математики. Одним из показателей кризиса стала так называемая "Теорема о четыре цветах". И вот, насколько её формулировка была проста, и насколько сложно доказательство оказалось, меня удивило.

Началось всë (как я потом узнал) с одного английского господина в XIX веке. Он жил в английской колонии (вроде в Южной Африке), и у него было много свободного времени. И чтобы убить время, этот господин раскрашивал контурные карты графств своего Альбиона.

Раскрашивая свои картинки, он увидел некоторые закономерности, о которых позже написал в Англию своему знакомому математику (читаем внимательно, ато потом опять начнется "Тойота со скоростью света не гоняет") :

Чтобы раскрасить любую контурную карту так, чтобы государства имеющие протяженные границы (то есть у них границы - линии, а не точка) , были окрашены в разные цвета, требуется не более 4 цветов

Пара примеров, чтобы было понятнее:

Флаг Швеции, пять областей раскрашены в 2 цвета.

Изображение, содержащее несколько областей, раскрашено в 4 цвета, в 3 - не получится

Доказана эта теорема была только в 1976 году, потом ещё в 90-е и в 2005 году. А все потому, что указанные доказательства посчитали читерством (если я правильно понял, доказательство основано на том, что взяты всё возможные "минимальные элементы" сочетания границ на карте, и путем перебора комбинаций установлено, что закономерность соблюдается; далее доказано, что эти элементы все, и других на "картах" возникнуть не может).

Я здесь рассмотрел теорему для участка плоского двумерного пространства, тогда как есть формулировки и для искривлëнных (глобус, к примеру, карты, свёрнутые в трубочку). Для трёхмерного пространства подобного не существует, а вот пространство на одно измерение радует.

Всего хорошего.

Некоторые люди слышали, что при движении на скорости света "время летит медленнее". Более начитанные даже знают, что до скорости света вообще нельзя разогнаться. На этот вопрос математически отвечает формула, входящая в, так называемые, преобразования Лоренца и Специальная Теория Относительности (ровно та, которую и изучают обычно в школах). Формула такая:

В ней подразумевается два субъекта: 2-й движется относительно 1-го с постоянной скоростью V, преодолевая расстояние Х. И вот 1-й смотрит на часы (свои и движущегося товарища) и измеряет время t2 и t1 соответственно. Всякий раз будет получаться, что часы движущегося наблюдателя (2) будут идти тем медленнее, чем быстрее он движется (смотрим формулу) .

А при скорости, равной скорости света (и тут тоже вступает в дело математика) в знаменателе нашей дроби под корнем образуется 0. На него как бы делить нельзя... Но если очень хочется, то можно, потому что это не "ноль", а бесконечно малая величина. Если нечто поделить на бесконечно малую величину, то мы получим - бесконечно большую величину. В нашем случае это значит, что движущиеся часы в частности (и время в общем) остановится (правда, это с точки зрения неподвижного наблюдателя; тот, у кого эти часы на руке, не заметит ничего особого). Это является одним из двух препятствий, не позволяющих разогнаться до скорости света.

Если же скорость движения много меньше скорости света (как у дедовской Жиги), то получится, что часы показывают одинаковое время (в числителе - вычитаемое будет пренебрежительно мало, а в знаменателе появится корень из единицы).

А если мы вдруг превысим скорость света? Тогда у нашей дроби в знаменателе под корнем образуется отрицательное число. Из отрицательного числа извлечь квадратный корень нельзя, стало быть, скорость света мы не превысим...

Нельзя извлечь квадратный корень из отрицательного числа. Но, если очень хочется, то можно. Только число это будет комплексное, а объект, чьи параметры могут быть описаны такими числами учёные пока не нашли, как не искали.

P. S. Не судите строго, лежу в госпитале, делать мне нефиг.