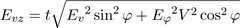DroidM

Как я вижу многие почему-то думают, что результат двухщелевого эксперимента меняется, потому что мы воздействуем детектором на фотоны/электроны и тем самым меняем их поведение. Все намного хуже или интереснее, в зависимости от отношения.

Возможно сюда придут специалисты по квантовой механике и поправят меня или вообще предадут анафеме, но объясняю как умею.

Начнем сначала.

Двухщелевой эксперимент:

1. Берем регистрирующий экран который может накапливать результаты попаданий фотонов.

2. Ставим перед ним другой экран с двумя близкорасположенными щелями.

3. Светим лазером на эти щели и свет пройдя через них образует на экране "зебру" из светлых и тёмных полос -- интерференционную картину.

Классическая волновая теория объясняет это просто -- каждая щель служит источником волны (ну или волна пройдя через 2 щели разделяется на две) и эти волны накладываются друг на друга. Там где на фиксирующем экране совпали максимумы волн появляются светлые полосы, там где минимумы -- темные. Согласно квантовой теории свет состоит из отдельных квантов -- фотонов и они обладают не только волновыми, но и корпускулярными свойствами, т.е. ведут себя как частицы. И объяснение результата эксперимента потребовало разработки математического описания поведения фотонов.

Теперь перейдем к модификации эксперимента и пояснению от квантовой механики.

1. Запускать фотоны стали строго по одному, т.е. с момента вылета и до момента прилета в фиксирующий экран фотон существует у нас в одиночестве.

2. Один фотон оставляет на экране одну точку, но при накоплении результатов, когда один за другим прилетает множество фотонов, на экране образуется классическая "зебра"  интерференционной картины из множества светлых и темных полос.

3. Получается, что один фотон (других в этот момент нет) прошел сразу через две щели и проинтерферировал сам с собой. Но фотон слишком мал чтобы пройти сразу через две щели, а расстояние между ними на порядки больше размера фотона. И тогда Фейнман (?) описал это так, что фотон движется не по одной траектории, а имеет множество разных траекторий с разной вероятностью и там куда траектории приводят с высокой вероятностью на экране светлые полосы, а там куда попасть вероятность близкая к нулю темные полосы. Как он сам говорил это только математическое описание.

4. У нас есть возможность экспериментально выяснить проходит фотон через одну щель или через обе. Все-таки эксперимент приоритетнее чем рассуждения. И это было проделано -- после экрана со щелями были поставлены детекторы один возле левой, другой возле правой. И эксперимент однозначно показал, что один фотон проходит через одну щель, потому что после излучения одиночного фотона срабатывал только один детектор либо правый либо левый. Но интерференционная картина при этом исчезала -- вместо "зебры" было только две ярких полосы по одной на против каждой щели. В квантовомеханическом описании когда мы узнаем положение фотона (неважно как узнаем) волновая функция схлопывается и фотон начинает вести себя как классическая частица и движется по одной конкретной траектории, а не по множеству траекторий с разной вероятностью.

И тут самое главное. Многие объясняют это тем, что мы воздействовали детектором на фотоны и этим изменили их поведение. Но это не совсем так, а точнее совсем не так. Если снова перейти к начальному варианту эксперимента когда лазер излучает непрерывным потоком фотоны триллионами, то никакие детекторы ничего не изменят, никакое воздействие детекторов на фотоны на результат не влияет -- интерференционная картина сохраняется. И позже напишу почему.

А теперь опять модифицируем эксперимент.

1. Для того чтобы определить через какую щель прошел фотон нам достаточно всего одного детектора потому, например, правый убираем. Если после излучения фотона детектор сработал то фотон прошел через левую щель, а если не сработал значит через правую. Т.е. прохождение фотона через правую щель мы определяем методом исключения.

2. Т.к. после правой щели у нас ничего нет, то и на фотоны там ничего не воздействует и тогда поведение правых фотонов не должно меняться и на против правой щели мы должны увидеть "зебру" из светлых и темных полос. Но ничего подобного, напротив правой щели мы увидим одну яркую полосу, точно такую же как и напротив левой.

3. Так что же случилось? Мы же никак не воздействовали на фотоны прошедшие через правую щель, но они изменили свое поведение. А случилось схлопывание волновой функции (т.е. математической формулы). Формуле все равно каким образом вы узнали/зарегистрировали местоположение фотона -- воздействовали детектором как для левых фотонов или просто вычислили методом исключения как для правых. Мы узнали местоположение фотона и именно это изменило его поведение, даже если мы ни чем и никак на него не воздействовали.

Вот к такому неожиданному выводу приводит эксперимент -- детектор воздействует на математическую формулу, волновая функция схлопывается и фотон меняет свое поведение даже если мы никак с ним не взаимодействовали. И опять вернемся к самой первой версии эксперимента когда лазер излучает поток фотонов триллионами и почему детекторы никак не влияют на результат эксперимента и "зебра" сохраняется -- дело в том, что мы не знаем через какую щель прошел каждый конкретный фотон. У нас есть просто статистика, что половина фотонов прошла через левую щель, а половина через правую, но местоположение каждого фотона не определено, а потому волновая функция не схлопывается и фотон ведет себя как волна. И никакие детекторы своим вмешательством ничего не меняют.

Знание о том где находится фотон, даже если вы это просто вычислили никак на фотон не воздействуя меняет результат эксперимента. Именно отсюда почти столетний хайп об "эффекте наблюдателя". Потому что если бы все было лишь в прямом воздействии приборов на частицу, то в этом ничего удивительного бы не было, а было бы все строго логично и ожидаемо.

Не "превысить невозможно", а "не наблюдаем в окружающей нас вселенной процессов, где информация передаётся быстрее скорости света". И вот отсюда уже понавыводили "законов" и "постулатов", чтобы всё сходилось.

А вот и воинствующие неучи подъехали... они не то что школьной физики не знают, они даже истории физики не знают. Сообщаю, что 200 лет назад тоже ничего быстрее света не видели, но ни у кого не было сомнений, что скорости могут быть сколь угодно большими, потому что есть галилеевское сложение скоростей. Из этой формулы V=V1+V2 прямо вытекает, что скорость может быть сколь угодно большой и для этого ничего "видеть" не надо. И тут "вдруг" в начале 20 века наложили ограничение на скорость. Не подскажете из-за чего? Что такого изменилось? Хотя вы точно не подскажете. Потому поясняю...

Примерно в середине 19 века Максвеллом была создана электродинамика благодаря которой у нас есть электричество, радиосвязь и вообще электроника, в т.ч. компьютеры и мобилы с которых вы сюда пишите. И вот у этой электродинамики возникла одна серьезная проблема и одна странность: 1) проблема -- электродинамика работала только в покоящейся системе отсчета, при попытке посчитать для движущейся ИСО получалась полная хрень которая противоречила реальности.

2) странность -- из уравнений Максвелла выводилась скорость электромагнитных волн в вакууме (да, у скорости С есть формула) и эта скорость была константой, она не зависела от ИСО.

В конце 19 века Майкельсон с Морли поставили свой опыт по обнаружению светоносного эфира, скорость света должна была быть разной в разных направлениях (по ходу движения Земли, против и поперек). Опыт показал, что скорость света не зависит от направления и скорости движения Земли.

Таким образом экспериментально было выяснено, что скорость света в вакууме не зависит от ИСО, в отличие от других объектов, свет во всех ИСО движется с одной и той же скоростью, скорость С не складывается ни с какой другой. И именно из этого экспериментального факта вытекает предельность С -- если С не зависит от ИСО (а это так) то она предельна, а если С не предельна, то она должна зависеть от ИСО (а это не так).

И самое интересное, что статья Эйнштейна по СТО называлась "К электродинамике движущихся тел". Именно СТО спасла электродинамику, переход в другую систему отсчета по формулам в которых прямо заложена предельная скорость С (преобразования Лоренца) привел к тому, что все расчеты прекрасно совпадали с реальностью.

Квантовая запутанность - очевидно один из таких читов

Не несите, пожалуйста, бред. Квантовая механика прямо запрещает передачу информации через квантовую запутанность, гуглите no-communication theorem

Стрельба всегда сопровождается ошибками.

Поговорим об ошибках стрельбы — конкретно об ошибках подготовки исходных данных и влиянии на них баллистики патрона.

Основными ошибками подготовки данных являются:

1. Ошибка определения дальности до цели. Опытный стрелок определяет дальность (без приборов) со срединной ошибкой 10%, средний — 15%.

2. Ошибка определения скорости ветра. Срединная ошибка составляет 1,5 м/с.

3. Ошибка определения скорости цели — 20%.

4. Ошибка определения курсового угла цели — 10° или 0,17 радиана.

Ошибка определения дальности. Итак, стрелок глядя на бегущую фигуру (мишень №8) определил, что дальность до цели 500 метров и выставил прицел 5. Это совершенно не означает, что до цели 500 метров, если стрелок опытный то срединная ошибка составит 10% или 50 метров. Таким образом цель будет находится в интервале 450-550 метров с вероятностью 0,5, т.е. в половине случаев. Естественно, что в другой половине случаев, т.е. с вероятностью 0,5, цель будет находится вне этого интервала. Как ближе (вероятность 0,25), так и дальше (вероятность 0,25) этого интервала.

Пока все сказанное никак не зависит от оружия в руках стрелка, но настала пора определить отклонение СТП из-за этой ошибки. Как ни странно, но пули летают по кривой и превышение траектории над линией прицеливания прямо зависит от баллистики оружия, точнее в очень большой степени определяется патроном. Численно вертикальное отклонение СТП равно ошибке дальности умноженной на тангенс угла падения пули на дистанции выставленного прицела (т.е. в данном случае 500 м). Сам угол можно взять из основной таблицы оружия или определить сразу тангенс из таблицы превышения траекторий. Рассмотрим АКМ и АК74:

Из таблицы превышений АКМ видно, что на 450 м (с прицелом 5) превышение 0,55 метра, а на 550 м понижение -0,83 метра. Таким образом за 100 м пути пуля падает на 1,38 метра, т.е. тангенс tg=(0,55-(-0,83))/100=0,0138. Умножим на ошибку в 50 метров и получим 50*0,0138=0,69 метра. С вероятностью 0,5 СТП отклонится по вертикали не более чем на 0,69 метра. С вероятностью 0,54 отклонение не выйдет за вертикальный габарит цели. (от центра до края цели 0,75 метра).

Из таблицы превышений АК74 видно, что на 450 м (с прицелом 5) превышение 0,31 метра, а на 550 м понижение -0,42 метра. Таким образом за 100 м пули пуля падает на 0,73 метра, т.е. тангенс tg=(0,31-(-0,42))/100=0,0073. Умножим на ошибку в 50 метров и получим 50*0,0073=0,365~0,37 метра. С вероятностью 0,5 СТП отклонится по вертикали не более чем на 0,37 метра. С вероятностью 0,83 отклонение не выйдет за вертикальный габарит цели.

Как видно баллистика влияет на отклонение пули из-за ошибки определения дальности. На малых дистанциях отклонения пули малы сразу по двум причинам: а) малы ошибки, 10% от 200 метров и 10% от 500 это совершенно разные величины; б) на малых дальностях углы падения также малы. Но с ростом дальности ошибки быстро растут и разница между АК74 и АКМ становится все больше. Тут можно вспомнить и стрельбу на большие дальности, важнейшим условием результативности которой является очень точное измерение дальности до цели и скорости ветра, что без приборов практически невозможно. Какой толк от винтовки с "субминутной" кучностью на дальности 1000 м если у Вас нет дальномера и ошибка в определении дальности, в лучшем случае, составляет ±100 метров?

Ошибка определения скорости ветра. Зная срединную ошибку — 1,5 м/с, можно определить боковое срединное вероятное отклонение пули на определенной дальности. Для этого нам понадобится таблица поправок на изменение метеоусловий из все того же НСД или таблиц стрельбы ГРАУ. Итак, все те же АКМ и АК74, дистанция 500 метров:

Из таблички для АКМ видно, что на 500 м снос ветром 10 м/с равен 3,4 метра, тогда снос ветром 1,5 м/с равен 3,4/10*1,5=0,51 метра. Т.е. с вероятностью 0,5 СТП отклонится в боковом направлении на расстояние не более 0,51 метра или с вероятностью 0,26 отклонение не выйдет за габарит цели (от центра до края цели 0,25 метра.).

Из таблички для АК74 видно, что на 500 м снос ветром 10 м/с равен 2,18 метра, тогда снос ветром 1,5 м/с равен 2,18/10*1,5=0,33 метра. Т.е. с вероятностью 0,39 отклонение не выйдет за габарит цели.

Как и в случае с определением дальности на малых дистанциях отклонения достаточно малы, но с ростом дальности сильно увеличиваются.

Ошибка определения скорости цели. Численно равна Еv=0,2Vц. В этот раз возьмем дистанцию поменьше, 300 метров думаю хватит. Бегущая фигура перемещается поперек линии стрельбы со скоростью Vц=3 м/с на дистанции 300 метров. Ошибка определения скорости 20%, т.е. 0,2Vц=0,6 м/с. Боковое отклонение пули численно равно подлетному времени пули умноженному на ошибку 0,2tVц. И на величину этой ошибки также оказывает влияние баллистика, а конкретно подлетное время пули которое можно взять из основной таблицы в НСД.

Для АКМ табличка дает t=0,52 с, таким образом бовокое отклонение составит 0,2*0,52*3=0,31 метра. С вероятностью 0,41 отклонение не выйдет за габарит цели.

Для АК74 t=0,39 с. Бовокое отклонение составит 0,2*0,39*3=0,23 метра. С вероятностью 0,54 отклонение не выйдет за габарит цели.

Ошибка определения курсового угла цели. Eφ=0,17 радиан. Рассмотрим случай стрельбы по цели перемещающейся под углом к линии стрельбы. Дистанция 300 м, бегущая фигура перемещается со скоростью 3 м/с под углом φ=45°. Тогда боковое отклонение пули будет складываться из ошибки определения скорости цели и ошибки определения курсового угла по следующей формуле

при угле φ=45° sinφ=cosφ=0,707. Как не трудно увидеть выражение под корнем не зависит от баллистики, зато подлетное время t зависит. Выражение под корнем будет равно 0,6^2*0,707^2+0,17^2*3^2*0,707^2=0,31, кв. корень 0,31=0,557 метра.

Для АКМ Evz=0,557t=0,557*0,52=0,29 метра. С вероятностью 0,44 отклонение не выйдет за габарит цели.

Для АК74 Evz=0,557t=0,557*0,39=0,22 метра. С вероятностью 0,56 отклонение не выйдет за габарит цели.

Основной вывод — баллистика оружия оказывает большое влияние на вероятность попадания в цель по причине меньшего отклонения пуль из-за ошибок подготовки исходных данных. 5,45-мм автоматная пуля обладает более настильной траекторией, меньшим ветровым сносом и меньшим подлетным временем чем 7,62-мм автоматная пуля, в значительной степени именно эти факторы позволяют АК74 стрелять эффективней АКМа. Меньший импульс отдачи и вес патрона не относится к ошибкам подготовки, но забывать о этих факторах не стоит.

Понять смысл, цели и итоги конкурса «Абакан» – какие требования выдвигались, откуда они взялись и почему именно такие, – без краткой истории создания 5,45-мм автоматного патрона сложно, а не пытающимся глубоко вникнуть в тему и невозможно. Данный пост практически полностью состоит из цитат Главы 6, 3 тома монографии Дворянинова.

Начало работ по отечественному малоимпульсному патрону относится к 1959 году когда в НИИ-61 было доставлено два американских 5,6-мм патрона, по одному из которых были воспроизведены чертежи и начаты исследования. В воспроизведенном патроне использовалась гильза от отечественного 5,6-мм охотничьего патрона. Партия воспроизведенных патронов была отправлена на Щуровский полигон для оценки убойного действия пуль стрельбой по мастичным мишеням.

В результате этих стрельб в/ч 01773 пришла к выводу:

на участке устойчивого движения пуля типа «Ремингтон» уступает по убойному действию пуле патрона обр. 1943 года на 11,5% на дальности 125 м и на 14% на дальности 425 м;

на участке неустойчивого движения она превосходит пулю патрона обр. 1943 года в 2,2 раза на дальности 125 м и в 3,5 раза на дальности 425 м.

Испытания на полигоне в/ч 33491 под Ленинградом в начале 1961 г. опытных вариантов 5,6-мм патронов показали:

По убойному действию были получены выводы, аналогичные выводам 1959 года: на участке устойчивого движения убойное действие пуль варианта В-2 и пуль патрона обр. 1943 года практически одинаковое; на участке неустойчивого движения зона поражения пулей калибра 5,6-мм значительно больше.

По результатам испытаний на пробивное и проникающее действие 5,6-мм пуль со стальным сердечником были сформулированы следующие выводы: «Из анализа результатов определения пробивного действия 5,6-мм патронов следует, что при стрельбе по одним преградам (стальной лист, пакеты из 25-мм сосновых досок) пули 5,6-мм патронов имеют несколько большее пробивное действие, чем пули патронов обр. 1943 года. При стрельбе по другим преградам пробивное действие пуль 5,6-мм патронов или практически одинаковое (по кирпичной стенке) или несколько меньше (по деревянным брусьям и песчаной преграде). Существенного различия в пробивном действии 5,6-мм пуль со стальными сердечниками с начальными скоростями 870 и 1000 м/с не имеется. Обобщая эти данные, можно сделать вывод, что по пробивному действию пуль 5,6-мм патроны и патроны обр. 1943 года практически равноценны».

Требования к автомату.

В 1962 году была начата НИР №Л-109-62 «Исследование путей создания нового патрона для автомата и ручного пулемета» (шифр «Легкость») и НИР НВ10-215-62 «Исследование путей разработки нового патрона для автомата и ручного пулемета с целью повышения ДЭС, уменьшения веса и увеличения маневренности оружия». Руководителем работ (совместно с НИИ-61) был назначен начальник 3 отделения 5 отдела подполковник к.т.н. Шерешевский Михаил Соломонович. Именно Шерешевский внес наибольший вклад в теоретическое обоснование тактико-технических требований к новому стрелковому комплексу. Высокая мобильность войск приводила к высокому темпу боевых действий и обуславливала необходимость в наличии легкого, маневренного автоматического оружия, обеспечивающего достаточную эффективность при стрельбе из малоустойчивых и неустойчивых положений – стоя с руки, с колена. Возможность применения противником тактического ядерного оружия привела к повышенному рассредоточению подразделений и вызвала необходимость в повышении дальности эффективной стрельбы. Тактически необходимые ДЭС для автомата были определены:

В обороне – 550-600 метров, стрельба с упора по характерной цели – «бегущий стрелок». Характерное время появления целей 3-5 с.

В наступлении – 250 метров, стрельба стоя с руки по характерным целям – «головная», «пулемет». Характерное время появления целей 3-5 с.

Дальность эффективной стрельбы.

Дальность эффективной стрельбы – расстояние, на котором с заданной вероятностью обеспечивается поражение цели одной очередью выстрелов или одним одиночным выстрелом из стрелкового оружия.

ГОСТ 28653-90 Оружие стрелковое. Термины и определения.

При определении ДЭС самым главным является критерий гарантийной вероятности при которой стрельба считается эффективной. Опыт войн XX века и особенно Великой Отечественной войны показал, что успешные действия пехоты противника срываются, когда процент пораженной силы составляет 40-50%... А уменьшение численности противника вдвое уменьшает его «боевую силу» примерно в 4 раза. Так же из опыта известно, что в бою стрелок успевает обстрелять цель в среднем 2-3 раза. Поэтому для оценки эффективной очереди целесообразно принять вероятность поражения равную 0,25. Эта вероятность при двух очередях обеспечивает гарантию 0,44, при трех – 0,58, а при четырех – 0,68. Это – достаточная гарантия для стрелкового оружия.

Дальность эффективной стрельбы (ДЭС) из данного образца стрелкового оружия – это дальность, на которой вероятность попадания характерной очередью для этого образца оружия равна 0,25, при стрельбе в типичных условиях по типичной цели.

Для оценки ДЭС из штатных образцов оружия были приняты следующие исходные данные:

вероятность поражения одной характерной очередью (5 выстрелов из автомата и 7 из ручного пулемета) равна 0,25;

характеристики рассеивания для АКМ и РПК табличные, для ПК – опытные, с выделением первых выстрелов очереди;

срединные ошибки в определении дальности до цели – 10%, скорости бокового ветра – 1,5 м/с, наводки – 1 т. д. в каждом направлении.

Расчетные средневзвешенные ДЭС из штатных образцов оружия по типичным целям составили, м:

Оружие Наступление Оборона

АКМ______95___________425

РПК______275__________395-535

ПК_______290__________420-600

Анализ путей повышения эффективности стрельбы из автомата на малые дальности (в наступательном бою) показал, что увеличение настильности траектории не приводит к существенному росту эффективности т.к. на малых дальностях ошибки подготовки данных малы. Единственным путем повышения эффективности является уменьшение рассеивания выстрелов, оптимальное рассеивание для 5-пульной очереди равно Вв=Вб=0,5 тысячных. Однако при при увеличении рассеивания до 1 тысячной вероятности попадания изменяются мало – на 0,02-0,04, поэтому пределы оптимального рассеивания 0,5-1 т.д.

При стрельбе в оборонительном бою оптимальное рассеивание выстрелов составляет 0,5-0,8 т. д. (ДЭС – 485 м), но оптимального рассеивания недостаточно для повышения ДЭС до тактически необходимых 550-600 м, необходимо повышение настильности траектории до ДПВ ≥410 м. Таким образом перспективный автоматный патрон должен иметь дальность прямого выстрела по грудной не менее 410 метров и при стрельбе короткими очередями стоя с руки обеспечивать срединное отклонение выстрелов не более 1 т. д. (на дальности 100 м Св=Сб≤30 см)

PS 5,45-мм патрон обеспечил требуемую баллистику, но обеспечить оптимальное рассеивание короткими очередями не смог, для этого требовались другие схемы автоматики.