Сечения: часть два
Всем привет! На связи снова Маша – репетитор по математике. В этот раз поговорим про тип сечений, который чаще всего приходится строить на ЕГЭ. Это сечения, плоскость которых задается точкой/прямой и условием. Все чертежи честно позаимствованы мной из прекрасного приложения Стереометрия AR (Stereometry AR на айфонах), разработчики, не ругайтесь.
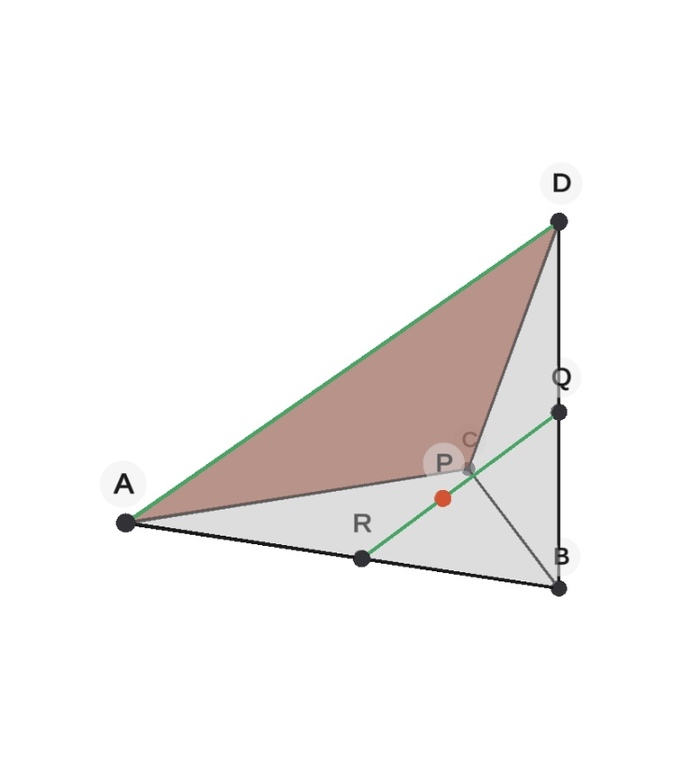
1) Допустим, у нас есть треугольная пирамида, и нас просят построить сечение, параллельное плоскости ACD (красненькая на чертеже) и проходящее через точку Р (тоже красненькая), лежащую на плоскости ABD.
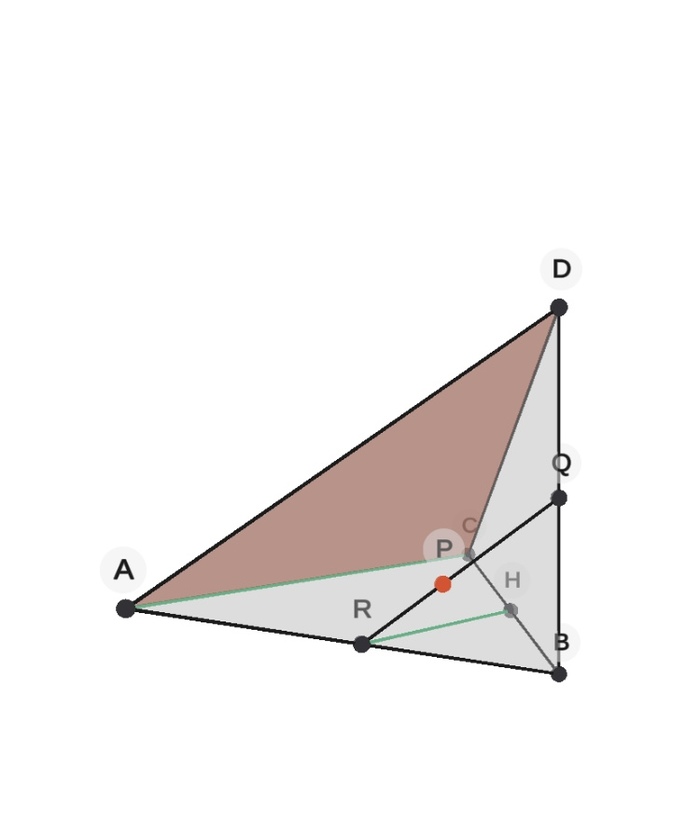
2) Через точку P проводим прямую, параллельную прямой AD. Нас интересуют точки пересечения проведенной прямой и прямых AB и BD. Назовем их R и Q соответственно. Теперь у нас есть точки, лежащие в плоскостях АВС и ВСD. Нам они нужны для дальнейшего построения.
3) Повторяем предыдущий пункт с прямой АС и точкой R. Получаем точку Н – пересечение проведенной прямой и прямой ВС.
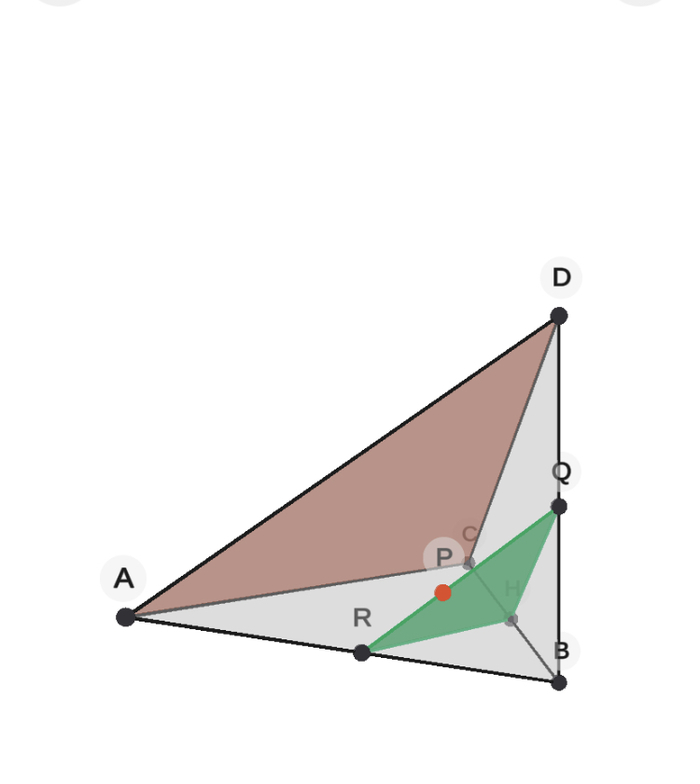
4) Соединяем точки Н и Q. Это легально, ведь они принадлежат одной плоскости ВСD. Ура, мы построили сечение (зелененькое на рисунке)!
P.S. По мотивам комментариев к моему предыдущему посту:
1) То, что я назвала метод построения методом следов связано с тем, что многие называют использованный мной прием методом следов. Если строго придерживаться терминологии, то это, конечно, не совсем так.
2) Сечение построено верно, использованный мной шорткат легален.
Всем добра и хороших оценок!