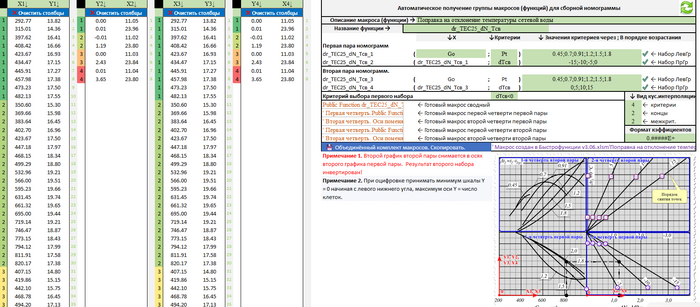
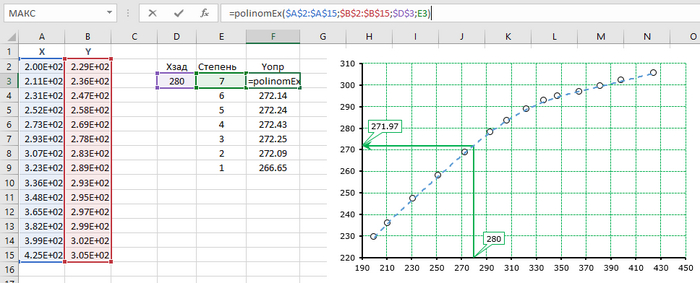
Ну а теперь пройдём все шаги вместе.
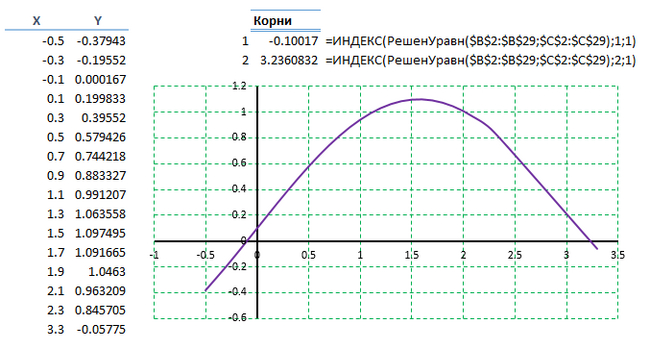
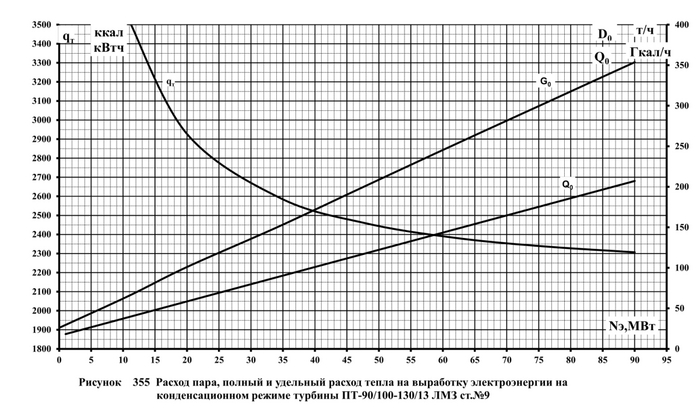
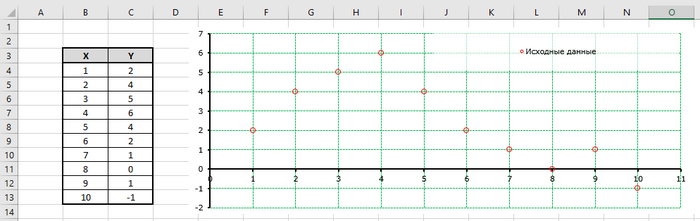
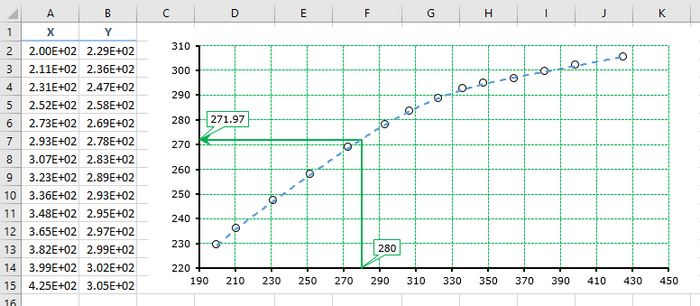
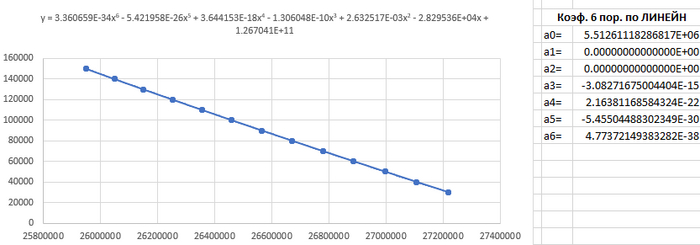
В прошлом посте я говорил про макрос расчёта на основании построения тренда.
====
' Апроксимация полиномом для всего массива исходных данных
' В подпрограмму передаются все заданные точки и апроксимация ведётся по всем точкам!
' Данные из листа Excel
Public Function polinomEx_all(xVal As Range, yVal As Range, x As Single, Optional stepen As Long = 2) As Variant
Dim i As Integer
' Проверка требования "число элементов массива на 1 больше чем степень полинома"
If xVal.Count < stepen + 1 Then
stepen = xVal.Count - 1
End If
polinomEx_all = 0#
Select Case stepen
Case 1 ' Уравнение а·х+b
For i = 1 To stepen + 1
polinomEx_all = polinomEx_all + (x ^ (stepen + 1 - i)) * Application.Index(WorksheetFunction.LinEst(yVal, xVal, True, True), 1, i)
Next i
Case 2 ' Уравнение а·х^2+b·x+c
For i = 1 To stepen + 1
polinomEx_all = polinomEx_all + _
(x ^ (stepen + 1 - i)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2)), True, True), 1, i)
Next i
Case 3 ' Уравнение а·х^3+b·x^2+c·x+d
For i = 1 To stepen + 1
polinomEx_all = polinomEx_all + _
(x ^ (stepen + 1 - i)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3)), True, True), 1, i)
Next i
Case 4 ' Уравнение а·х^4+b·x^3+c·x^2+d·x+e
For i = 1 To stepen + 1
polinomEx_all = polinomEx_all + _
(x ^ (stepen + 1 - i)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4)), True, True), 1, i)
Next i
Case 5 ' Уравнение а·х^5+b·x^4+c·x^3+d·x^2+e·x+f
For i = 1 To stepen + 1
polinomEx_all = polinomEx_all + _
(x ^ (stepen + 1 - i)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5)), True, True), 1, i)
Next i
Case 6 ' Уравнение а·х^6+b·x^5+c·x^4+d·x^3+e·x^2+f·x+g
For i = 1 To stepen + 1
polinomEx_all = polinomEx_all + _
(x ^ (stepen + 1 - i)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5, 6)), True, True), 1, i)
Next i
Case 7 ' Уравнение а·х^7+b·x^6+c·x^5+d·x^4+e·x^3+f·x^2+g·x+h
For i = 1 To stepen + 1
polinomEx_all = polinomEx_all + _
(x ^ (stepen + 1 - i)) * Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5, 6, 7)), True, True), 1, i)
Next i
Case Else
End Select
End Function
====
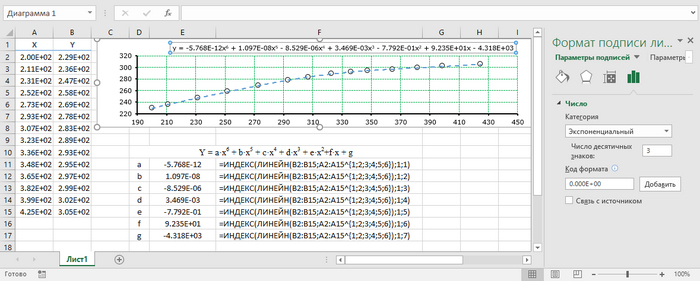
Как видно - ничего сложного в этом макросе нет. В соответствии с заявленной степенью полинома происходит перемножение заданного Х в соответствующей степени на соответствующий коэффициент полинома. Коэф-ты вычисляются точно так же как вычислялись на листе экселя.
Т.е.
WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4)), True, True)
полностью совпадает с
ЛИНЕЙН(Y; X{1;2;3;4}; True; True)
Ну а теперь просто заменим расчёт на составление текстовой переменной
=====
' Апроксимация полиномом для всего массива исходных данных
' В подпрограмму передаются все заданные точки и апроксимация ведётся по всем точкам!
' Данные из листа Excel
' Результат работы программы - текст (уравнение полинома)
Public Function polinomExStr(ByVal xVal As Range, ByVal yVal As Range, Optional stepen As Long = 2) As Variant
' Проверка требования "число элементов массива на 1 больше чем степень полинома"
Dim i As Integer
If xVal.Count < stepen + 1 Then
stepen = xVal.Count - 1
End If
polinomExStr = ""
Select Case stepen
Case 1 ' Уравнение а·x+c
For i = 1 To 2
polinomExStr = polinomExStr & " + X ^ " & (2 - i) & " * " _
& Format(Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1)), True, True), 1, i), "0.###E+")
Next i
Case 2 ' Уравнение а·х^2+b·x+c
For i = 1 To 3
polinomExStr = polinomExStr & " + X ^ " & (3 - i) & " * " _
& Format(Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2)), True, True), 1, i), "0.###E+")
Next i
Case 3 ' Уравнение а·х^3+b·x^2+c·x+d
For i = 1 To 4
polinomExStr = polinomExStr & " + X ^ " & (4 - i) & " * " _
& Format(Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3)), True, True), 1, i), "0.###E+")
Next i
Case 4 ' Уравнение а·х^4+b·x^3+c·x^2+d·x+e
For i = 1 To 5
polinomExStr = polinomExStr & " + X ^ " & (5 - i) & " * " _
& Format(Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4)), True, True), 1, i), "0.###E+")
Next i
Case 5 ' Уравнение а·х^5+b·x^4+c·x^3+d·x^2+e·x+f
For i = 1 To 6
polinomExStr = polinomExStr & " + X ^ " & (6 - i) & " * " _
& Format(Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5)), True, True), 1, i), "0.###E+")
Next i
Case 6 ' Уравнение а·х^6+b·x^5+c·x^4+d·x^3+e·x^2+f·x+g
For i = 1 To 7
polinomExStr = polinomExStr & " + X ^ " & (7 - i) & " * " _
& Format(Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5, 6)), True, True), 1, i), "0.###E+")
Next i
Case 7 ' Уравнение а·х^7+b·x^6+c·x^5+d·x^4+e·x^3+f·x^2+g·x+h
For i = 1 To 8
polinomExStr = polinomExStr & " + X ^ " & (8 - i) & " * " _
& Format(Application.Index(WorksheetFunction.LinEst(yVal, Application.Power(xVal, Array(1, 2, 3, 4, 5, 6, 7)), True, True), 1, i), "0.###E+")
Next i
Case Else
End Select
End Function
=====
Ну или немного в другом виде с учётом ряда особенностей и модификаций
=====
' Программа формирования текста макроса для функции одного уравнения
Public Function fun_macros_Y(xVal As Range, yVal As Range, PolyStep As Long, _
Optional Name_f As String = "Nomogramma", _
Optional Opisanie As String = " Уравнение ", _
Optional NameX As String = "Xisk") As Variant
Dim j As Long
Dim N As Long
Dim k As Long
Dim stepen As Long
Dim xn() As Double ' заявляем массив X
Dim yn() As Double ' заявляем массив Y
Dim c() As Double ' заявляем массив c - коэффециенты уравнения полинома
fun_macros_Y = "" & Chr(10) & "' " & Opisanie & Chr(10)
fun_macros_Y = fun_macros_Y & "Public Function " & Name_f & "(ByRef " & NameX & " As Single) As Variant" & Chr(10)
Dim Nna4 As Long 'Номер начала диапазона.
Dim Nkon As Long 'Номер конца диапазона.
Nna4 = 1
Nkon = xVal.Count
' Проверяем на соответствие число элементов участка степени полинома
If (Nkon - Nna4) < PolyStep Then
stepen = (Nkon - Nna4)
Else
stepen = PolyStep
End If
' Заполняем матрицы участка
ReDim xn(1 To (Nkon - Nna4 + 1), 1 To stepen)
ReDim yn(1 To (Nkon - Nna4 + 1), 1 To 1)
ReDim c(1 To stepen + 1) As Double
For j = 1 To (Nkon - Nna4 + 1)
xn(j, 1) = xVal.Rows(j + Nna4 - 1)
For N = 2 To stepen
xn(j, N) = xn(j, 1) ^ N
Next N
yn(j, 1) = yVal.Rows(j + Nna4 - 1)
Next j
' Делаем расчёт и вывод.
fun_macros_Y = fun_macros_Y & Name_f & " = "
For k = 1 To stepen + 1 Step 1
c(k) = Format(Application.Index(WorksheetFunction.LinEst(yn, xn, True, True), 1, k), "0.####E+")
If c(k) >= 0 And k > 1 Then
fun_macros_Y = fun_macros_Y & " + " & c(k)
Else
fun_macros_Y = fun_macros_Y & c(k)
End If
If (stepen + 1 - k) > 0 Then
fun_macros_Y = fun_macros_Y & " * " & NameX & " ^ " & (stepen + 1 - k) & " "
End If
Next k
fun_macros_Y = fun_macros_Y & Chr(10) & "End Function" & Chr(10)
End Function
=====
Макрос ждёт в качестве вводных данных:
xVal - столбец известных Х
yVal - столбец известных Y
PolyStep - желаемую степень уравнения. Если точек будет меньше чем требуется для степени - на уменьшится
Name_f - название получаемого макроса. Опционально. Если не задать будет Nomogramma
Opisanie - описание получаемого макроса. Опционально. Если не задать будет Уравнение
NameX - название/имя аргумента. Опционально. Если не задать будет Xisk
Вызов макроса:
=ПОДСТАВИТЬ(fun_macros_Y(X; Y; 3; "fun_пример"; "Пример создания макроса"; "Go");",";".")
=ПОДСТАВИТЬ( ;",";".") требуется для замены запятых на точки. Иначе будет казус - VBA в качестве разделителя целой и дробной части использует точку, а в текстом виде (по крайней мере в рус.экселе) разделитель запятая.
Обратите внимание, что
"fun_пример"; "Пример создания макроса"; "Go" - текстовые, т.е. заключаются в кавычки
"fun_пример"; "Go" - должны соответствовать требованиям к переменным. Т.е. не должны содержать пробелов, не должны совпадать с имеющимися переменными или названиями ячеек/диапазонов.
Результатом выполнения макроса будет (поставил 3-ю степень чтобы результат влез в окно поста):
"
' Пример создания простого макроса
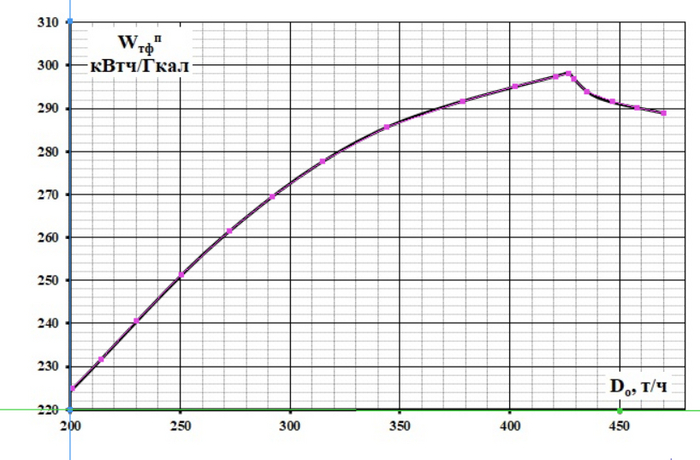
Public Function fun_Wтф(ByRef Go As Single) As Variant
fun_Wтф = 0.00000056401 * Go ^ 3 -0.001952 * Go ^ 2 + 1.3842 * Go ^ 1 + 25.341
End Function
"
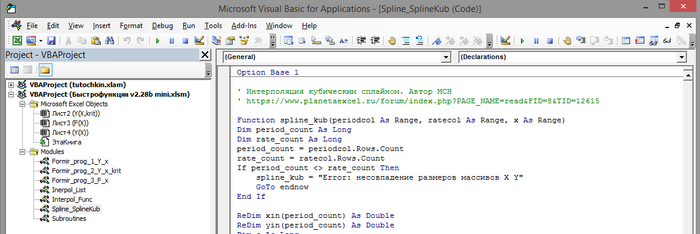
Останется скопировать данный текст в модуль VBA и удалить двойные кавычки в начале и конце текстовки.
Если есть желание повысить количество знаков коэффициентов - правим формат "0.####E+"
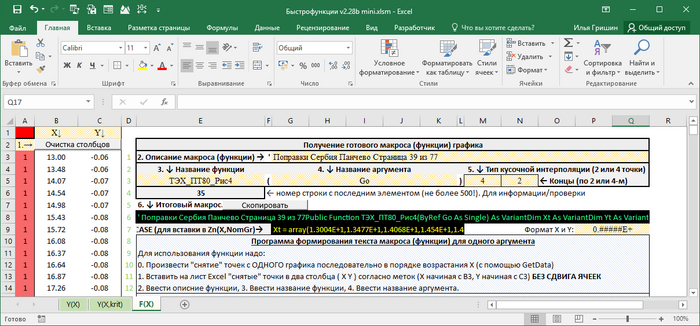
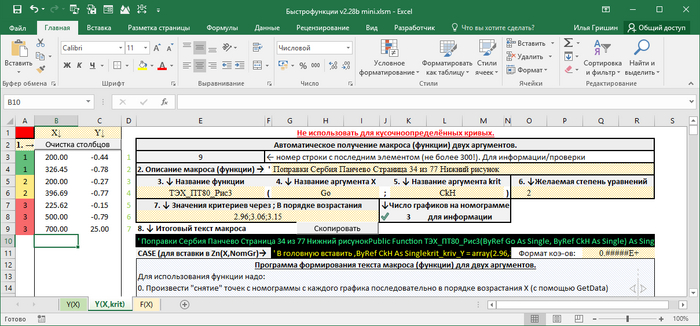
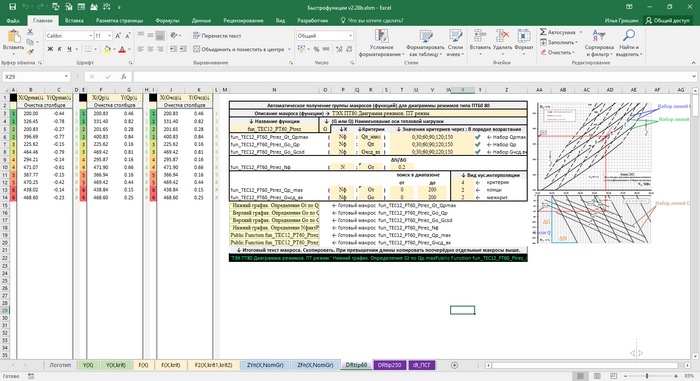
Для ускорения работы у меня собраны листы/шаблоны позволяющие не лезть в заполнение вызова макросов.
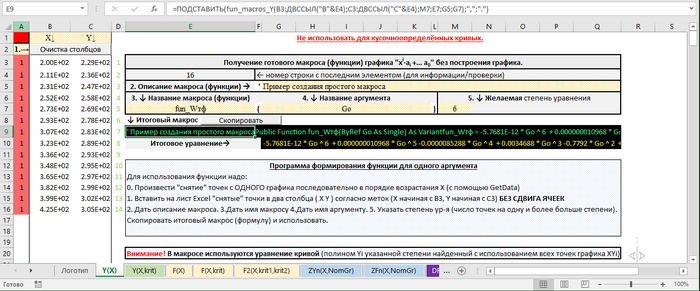
Вызов макроса для данного случая у меня выглядит так (в Е9):
=ПОДСТАВИТЬ(fun_macros_Y(B3:ДВССЫЛ("B"&E4);C3:ДВССЫЛ("C"&E4);M7;E7;G5;G7);",";".")