Продолжение поста «Аксиоматика множества призрачных чисел»
Место множества призрачных чисел относительно других множеств
Короче, для начала отметим, что для множества J 6-я аксиома, которая ∀a∈J\{0}: 0*a=0 избыточна. То что в ямайкамурровых числах 0 умножить на любой не 0 равно 0 выводится как следствие. Ну и ещё @alice9tails утверждает, что ∅ вообще по факту не операция. Ну я тоже подумал, что и фиг с ней. Так что в сухом остатке мы имеем множество J которое отличается от R только в следующих аксиомах (чтобы не переписывать всю эту аксиоматическую портянку, покажу только отличающиеся):
∀a,b∈J\{0}: a*b=b*a_________________∀a,b∈R: a*b=b*a
∀a∈J b,c∈J∖{0}: (a*b)*c=a*(b*c)_____∀a,b,c∈R: (a*b)*c=a*(b*c)
∀a,b∈J c∈J∖{0}: (a+b)*c=a*c+b*c____∀a,b,c∈R: (a+b)*c=a*c+b*c
∀a,b,c∈J c>0: (a⩽b⇒a*c⩽b*c)_______∀a,b,c∈J, c⩾0: (a⩽b⇒a*c⩽b*c)
@alice9tails натолкнула меня подумать, каково же место призрачных чисел в структуре математики. Пришлось смотреть теории множеств, коих, оказывается, в мире есть, и не одна. Собственно, я не особо нашёл что-то, что могло бы быстро и легко помочь с этим. И, скорее всего, именно что не нашёл, а не то, что его там нет. Я просто объясню суть терминов, которые буду использовать, чтобы было понятно. Но имейте в виду, что это всё, скорее всего, просто мой велосипед от какой-то из теорий множеств.
Множество элементов А является конкретным относительно множества B, если в нём определено как минимум одно дополнительное свойство для как минимум одного элемента множества В и при этом между всеми аксиомами множеств A и B нет противоречий. Множество В в таком случае можно считать абстрактным относительно А.
Определить дополнительное свойство элемента множества В, значит ввести аксиому о получении результата операции с этим элементом, который не определён для множества В.
Покажем на примере, что множество С является конкретным относительно R:
√(-1) - не определено в R
√(-1)=i - определено в С
Очевидно, что определено дополнительное свойство в виде результата для √-1, а значит, С конкретно относительно R, ну или, что тоже самое, R абстрактно относительно C. То, что у этих множеств нет конфликтов в аксиомах, доказано и без меня.
Теперь вернёмся к нашим баранам и покажем, что R конкретно относительно J:
a*0 - не определено в J, это при том, что 0*a=0, для a≠0
a*0=0 - определено в R
J вообще было получено просто вытравливанием коммутативности, ассоциативности и дистрибутивности умножения на 0 из R, так что конфликты искать не приходится.
Покажем, что G конкретно относительно J:
a*0 - не определено в J
a*0=g(-1)a - определено в G
При этом G не является R в силу того, что:
0*1/0 - не определено в R
0*1/0 = g(1)0 - определено в G
Логично тогда предположить, что G конкретно относительно R, но эти два множества имеют противоречие на уровне аксиом:
a*0=0 - в R (я знаю, что a*0=0 в R не аксиома, а следствие)
a*0=g(-1)a - в G при том, что 0=g(0)0
То есть свойства нулю из J эти множества добавляют разные.
Проще выражаясь: G конкретизирует J иначе, чем это делает R.
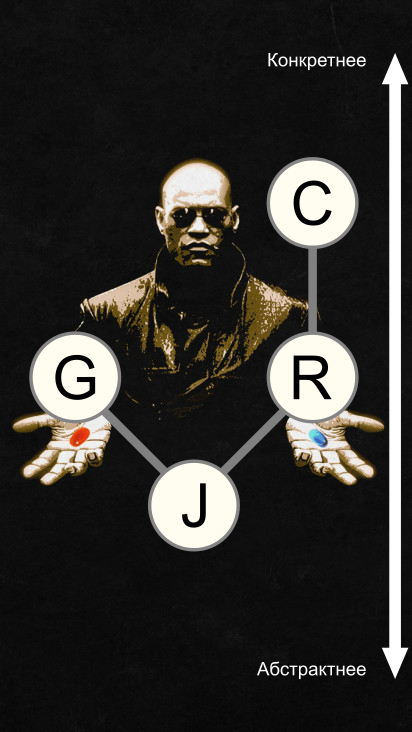
Я тут картиночку для наглядности запилил с иерархией этих множеств:
Вот у вас есть множество G для которого определены все его операции для всех чисел - и множество R у которого нет деления на 0. И при этом они оба идут от одного абстракта...
Я, конечно, понимаю, что человечество, тысячелетие с лишним просидевшее на R, итак прекрасно себя чувствует, но вопросик-то есть один: может ли так быть, что сегодня мы не имеем возможности описать что-либо математически только потому, что стираем информацию умножением на 0 и вообще не умеем на него делить?
Кстати, вполне возможно конкретизировать аналог множества комплексных чисел и от G. И все другие навороты, аналогичные тем, что есть для R, скорее всего, тоже.