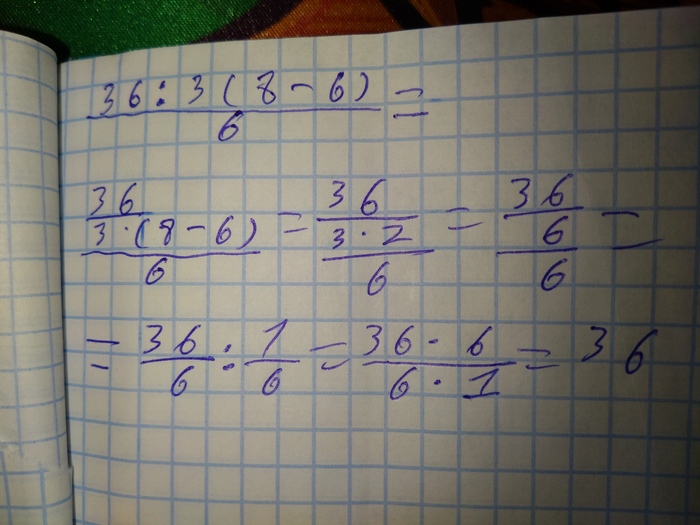То что утверждает этот инвестиционный цыган вовсе не верно. Выражение в посте, запишу его строчно, оно выглядит так:
(36:3(8-6)) / 6
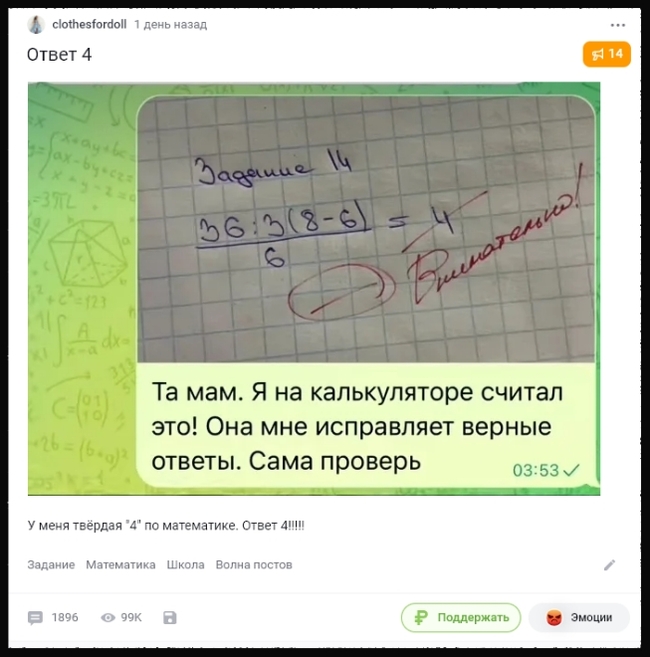
Оно записано правильно, хотя многие утверждают что данный пример лишен смысла и на него нет ответа, другие же вовсе решают неверно.
Запись 3(8-6) с точки зрения первоочередности неравна 3×(8-6). 3(8-6) является неделимым. Отсутствие знака * в выражении говорит о том что за скобки вынесен общий множитель.
Допустим: 8=a, а 6=b, следовательно выражение 3(8-6) до выноса множителя 3 за скобки будет выглядеть следующим образом: (3a-3b). ПОВТОРЮСЬ! ОТСУТСТВИЕ ЗНАКА × ГОВОРИТ О ТОМ ЧТО МНОЖИТЕЛЬ ОБЩИЙ И ВЫНЕСЕН ЗА СКОБКИ! И ЯВЛЯЕТСЯ СЛЕДУЮЩИМ ПО ПРИОРИТЕТНОСТИ РЕШЕНИЕМ ПОСЛЕ ДЕЙСТВИЙ В СКОБКАХ!!!
Отсутствие знака × является приоритетнее его наличия. Никакие скобки не нужны для выражения 3a как придумывает кладовочник. Это лишено смысла, так как оно является одним числом.
Для тех кто знаком с формальной стороной математики будет понятно. В аксиомах действительных чисел не вводится понятия "деления". Для чего это говорю, поясню. Когда что то выносят за скобки то имеют ввиду что нужно поделить то, из чего мы выносим на то, что выносим. В данном примере буду говорить что раскладываю на множители, которое не затрагивает процессы деления. Можно сказать, на какое число нужно умножить данное, чтобы получить исходное? Что само по себе верно. Вот пример: x^²+x=0, решения 2, x=0, x=-1 вынесем за скобки x, получим x(x+1)=0. Возьмем x=0, подставляем в выражение 0+0=0, нам ничего не мешает вынести 0 за скобки, получаем 0(1+1)=0. Аксиома гласит, умножение нуля на любое число дает ноль.
Выражение 3(8-6), логичное и выполняется первоочередной.
Так как 3 является общим множителем для выражения (24-18), вернёмся к нашему примеру и разберем порядок выполнения действий
(36:3(8-6)):6
1) 8-6=2
2) 3×2=6
3) 36:6=6
4) 6:6=1
Иного здесь нет, не нужно придумывать колесо со скобками, это придумали задолго до нас, и не стоить принимать утверждения публичных людей за чистую монету. Тяжело принимать тот факт, что подобное обсуждают огромное колличество людей и многие убеждены в ложном варианте. Условно сказать что половина комментаторов ГЛУПЫЕ, реально глупые в элементарных вопросах, а ведь кто то из них выполняет ответственную работу. А другой комментатор благодарит этого чупа-чупса у доски и вовсе упомянул что дочь скоро в школу пойдет и сожалеет что был не прав, и ведь будет же учить и многие учат основываясь на подобном. Что вырастет из усилий подобного воспитателя? Надеюсь такие большая часть не привлекается к подобной работе, принеси подай пошел ***** не мешай, вот ваша зона ответственности.

Про арксинус вы что-то загнули. Арксинус - это угол (в градусах или радианах)

#comment_342486181

Во-первых, арксинус - это как правило не угол, а число.

Многие выпускники это не вполне осознают, но не зря тригонометрия в школьном курсе делилась на два куска: сперва тригонометрия в треугольнике, на геометрии в 9 или даже 8 классе. И только потом тригонометрические функции, на уроках алгебры и начала анализа в 10 классе. Тригонометрические функции - функции от числа, а не угла, и их обратные - тоже числа, а не углы. Хотя их и можно трактовать как углы, радианная мера которых совпадает с соответствующим числом.

Во-вторых, значком "минус первой степени" нередко обозначается обратная функция вообще. Так и в России, и в США. Но в России обычно такая нотация вводится, когда с функциями начинают работать как с математическим объектом. Заметно это становится обычно в курсе матана, когда проходят производные. Тут чаще всего школьник/студент и встречает впервые запись типа

пусть x = f ⁻¹(y) = g(y), тогда g'(y) = 1 / f'(x)

И первым же примером часто рассматривают производную арксинуса.

Так что обозначать арксинус как sin⁻¹ резонно, и в Америке часто так и поступают. Тем более что американских школьников специально готовят, учат рассматривать функции как математические объекты. (Получается плохо, но это уже другой вопрос: когда десять лет ученики все больше отстают в базовой математике вплоть по элементарную алгебру, быстрый рывок в 11-12 классах в голове не укладывается.)

Ответ - Единица.

Я понимаю, как люди получают Четверку, но это не правильно.

Смотрите, когда Вы решаете 36:3(8-6) и сначала решаете в скобках 8-6, получив двойку, то запись не превращается в 36:3*2 ... потому, что арифметические действия внутри скобок это не открытие скобок, то есть совершив действия внутри скобок вы от них не избавились.

Когда я учился в школе, были простые правила открытия скобок, так при наличие у скобок множителя для их открытия, каждый элемент внутри скобок должен быть умножен на этот самый множитель:

a(b+c) = ab+ac

То-есть если записать 36:3(8-6) на уровне абстракции получим: x:a(b+c).... подойдите с этим к любому учителю математики и попросите преобразовать эту запись в более читабельный вид без скобок, он Вам напишет дробь, с X в числителе и ab+ac в знаменателе...

Поэтому ответ - Единица.

Так как вычисления внутри скобок это лишь вычисления внутри скобок, а не их открытие.

... Ну как минимум таким был математический синтаксис раньше.

То есть меня учили, что вот это 36:3*(8-6) нужно читать как 36:(3*(8-6))... а не так, как читают те кто получают 4, то есть: (36:3)*(8-6)...