Ответ на пост «Форма нашей планеты...»
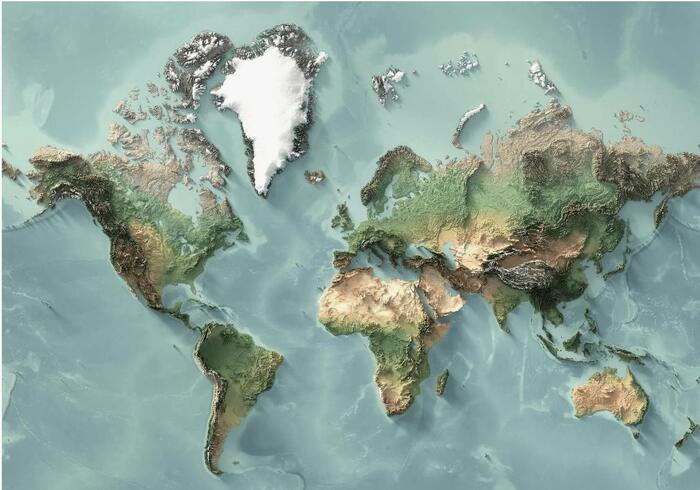
Масштабы нашей планеты столь велики, что все эти горы будут ничтожны на таких площадях. Вот карта рельефа России из интернетов.
Но на самом деле в таком масштабе большая часть рельефа России будет выглядеть вот так
Длина России с запада на восток ~10 000 км. Если, опять же, мы отмасштабируем её до такого листа железа со стороной в 1 метр, мы получим коэффициент в 10 000 000. Теперь по нему масштабируем Эльбрус и Байкал, как самую высокую и глубокую точку (возможно есть что-то глубже, но здесь это особой роли не сыграет). Пусть разница между пиком Эльбруса и Байкала будет даже в 10 000 метров. 10 000 ÷ 10 000 000 = 0,001 метр, то есть 1 мм — МАКСИМАЛЬНЫЙ перепад высот. Так что просто добавляете выступ где-то 0,6 мм в район Кавказа, 0,1 мм в район Байкала, что-то в районе 0,4 мм у Алтайских гор и тп.
*надеюсь нигде в нулях не запутался
Ответ на пост «Форма нашей планеты...»
Меня всегда прикалывали подобные картинки, но.. Меня перекрывает знание математики.
Сколько там диаметр земли?
Экваториальный диаметр составляет 12 756 км, но диаметр от полюса до полюса равен 12 710 км — разница 46 км.-яндекспоиск
Какая самая большая гора? сколько метров?
Эверест~8800м. (8.8км.)
Какая наибольшая глубина моря?
Марианская впадина~11000м.(11км)
Теперь представим себе землю в соотношении 1:1000 (или наоборот?)
Посчитаем? На 12.7 километров земли выпуклость самой большой горы всего 9(упрощенно) метров. Самая глубокая впадина-11 метров.
Это много! Уменьшаем! Еще в тысячу раз!
У нас глобус диаметром в 12 метров. на нем самая высокая гора возвышается на 9 миллиметров. А впадина? Она 11 миллиметров.
Вы видели такой глобус? Я- нет. Максимальный глобус, что я видел- 30 см. в диаметре.
Это 1к 40?
Теперь обЪясните мне, как я должен ощутить на этом глобусе перепады в 0.5-0.6 миллиметров? И как мне поверить во все всратые картинки зная математику?
Форма нашей планеты...
Давно думал написать это в одном посте, т.к. в разное время попадались отдельные сообщения или комментарии на тему формы планеты (эллипс или геоид), а также рельефности поверхности. Такое ощущение, что люди даже близко не представляют себе реальность. Попробую это исправить...

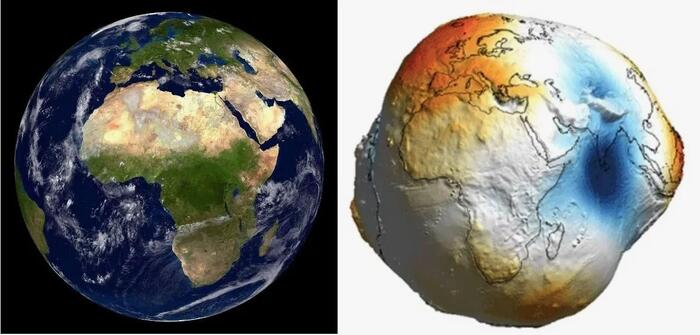
Я вот про эти дурацкие картинки, которая всем так понравилась...
Началось всё с того, что я решил купить ребёнку рельефный глобус или рельефную карту, которая наглядно показала бы причины выбора маршрутов переселения народов, военных походов и т.д.
Изучив предложенные варианты я понял, что на масштабах комнатных карт или глобусов горы получаются настолько утрированно огромными, что для их изображения значительно преувеличивается площадь подошвы горных массивов и некоторые регионы становятся горными вместо равнинных. Как наглядное пособие - неплохо, но как более-менее реалистичное отображение - вообще не то.
Такое положение меня немного не устроило и я решил попробовать самостоятельно изготовить глобус с реалистичным масштабом рельефа, ведь сейчас нет никакой сложности напечатать и раскрасить что угодно на 3D принтере. Взялся за анализ и понял, что занятие это почти бессмысленное. На масштабах глобуса в человеческий рост (2,0м в диаметре), глубина Марианской впадины получается 1,7мм.
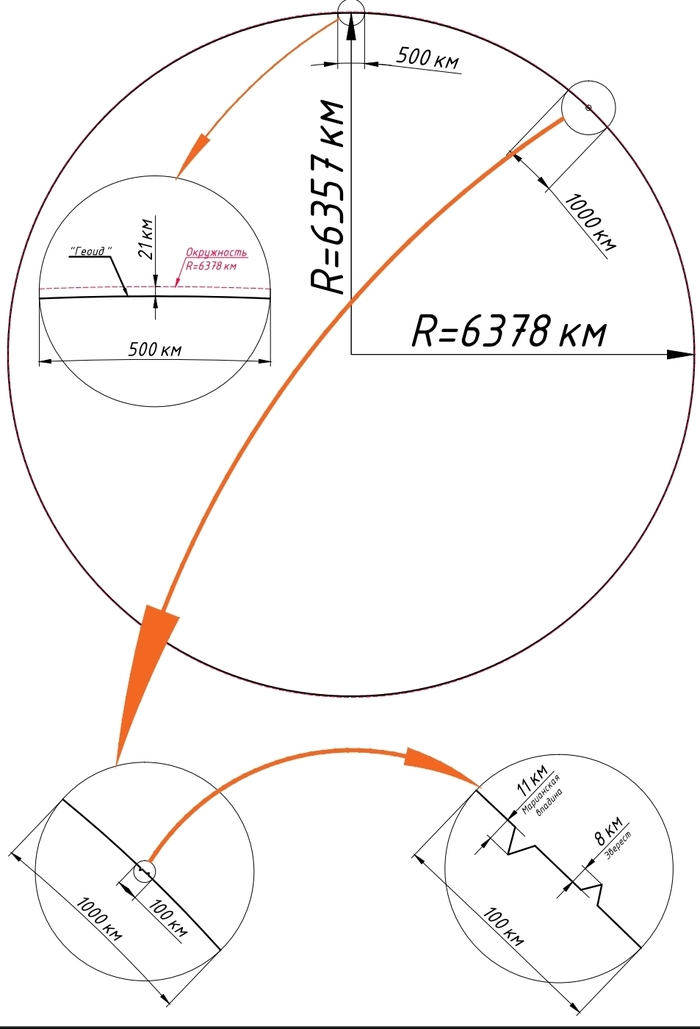
Что сподвигло меня прикинут вообще масштабы озвученных мифов про "не шарообразность" Земли, геоидную форму и т.д.. Нарисовал эллипс в миллиметрах с разными радиусами по вертикали и горизонтали, ожидая получит тот самый эллипс-геоид-овал...
Но по факту вышел круг с крошечной погрешностью в вертикальном и горизонтальном измерении - 0,2%.
Получается, что наша планета - совершенно идеальный шар с лёгкими шероховатостями в виде гор, каньонов, океанов...
В одном из обсуждений на эту тему я увидел аргумент, что "если разница диаметров есть, то, всё же, не шар". Ну, формально я согласен, действительно не шар. Но как можно понять это? Ведь на масштабах планеты это хоть как-то получается измерить, а как это измерить на понятных нам масштабах?
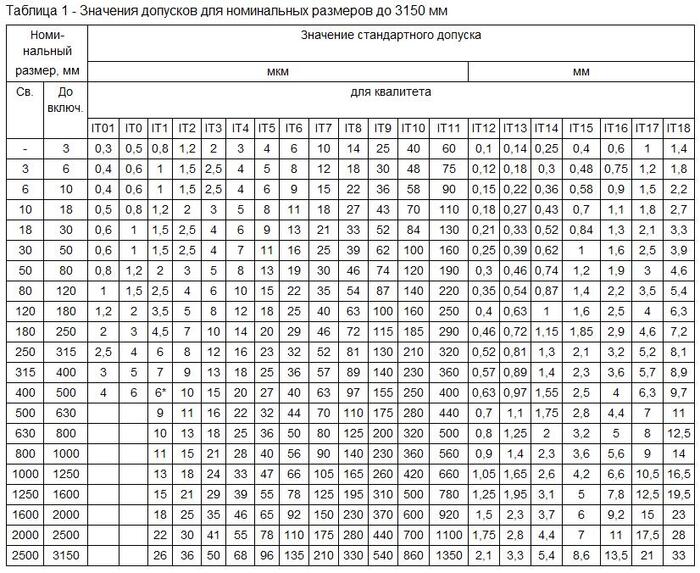
Есть такой ГОСТ 25346-2013 "Система допусков на линейные размеры. Основные положения, допуски, отклонения и посадки". Этот нормативный документ, в числе прочего, содержит таблицу допусков по квалитетам точности изготовления деталей разного назначения.
Таблица 1 из ГОСТ 25346-2013 "Система допусков на линейные размеры. Основные положения, допуски, отклонения и посадки"
Квалитет может быть разный, зависит он от требований к точности изготовления, а от квалитета зависит сложность изготовления, обработки детали и цена изготовления.
Квалитеты с 1 до 4-го используются для изготовления калибров и контркалибров.
Квалитеты от 5-го до 12-го применяют для изготовления деталей, образующих сопряжения (ГЦС).
Квалитеты от 13-го до 17-го используют для параметров деталей, не образующих сопряжений и не оказывающих определяющего влияния.
То есть, примерно на границе IT12-IT13 квалитета находится разница между машиностроительными требованиями к деталям для механизмов и обычными требованиями к качеству изготовления деталей для строительства и конструирования. То есть, контроль качества изготовления не мелкой (20-30см) детали при квалитете IT12 или IT13 доступен и понятен большинству населения - линейка, штангенциркуль, а при квалитетах ниже IT12 это уже микрометр на калиброванных столах для измерения - доступно не всем.
Возьмём для понятного примера футбольный мяч. Его наверняка держали в руках почти все.
Так вот, диаметр футбольного мяча - 22см, то есть 220мм, а это значит, что согласно квалитету IT12, точность изготовления металлического шара колеблется от 0,18%(для 250мм) до 0,26%(для 180мм) от линейного размера, при диаметре 220мм, точность нормального изготовления металлического шара - 0,214% от линейного измерения, то есть 0,47мм.
Сможет ли кто-то из нас без инструментов, "на глаз", оценить шарообразность футбольного мяча, если разница в диаметрах будет 0,47мм? Я сомневаюсь. Но тут спорить особого смысла нет.
С футбольным мячом есть ещё один интересный пример для понимания масштабов рельефа нашей планеты. Мы же все, наверняка, держали его в руках. Все видели на нём швы. Вот эти швы и будут отличной иллюстрацией для ощущения рельефа нашей планеты.
Для простоты расчёта предположим, что глубина шва на поверхности мяча - 1мм.
Диаметр футбольного мяча - 22см или 220мм.
Диаметр планеты Земля (возьмём экваториальный радиус из Википедии) - 12 756,2км или 12 756 200 000мм.
То есть, диаметр планеты Земля в 57 982 727,3 раза больше диаметра футбольного мяча. А значит, если бы шов на футбольном мяче являлся бы масштабной моделью каньона на поверхности планеты, то на теле нашей планеты такой каньон должен был бы быть 57,98км глубиной.
Даже если я ошибся в допущении и шов на футбольном мяче глубиной не 1,0мм, а 0,5мм, то каньон всё равно получается глубиной 28,99км.
То есть, Марианская впадина (до 11 км глубиной), если её масштабно изображать на поверхности футбольного мяча, должна быть глубиной 0,18мм - то есть просто ЦАРАПИНА НА КОЖЕ МЯЧА.
Как-то так...